หลังจากทิ้งเรื่องนี้ไป
๕ ปีเศษ (จากธันวาคม
๒๕๕๗)
ก็ได้เวลากลับมาเขียนเรื่องนี้ต่อ
คือ Memoir
ฉบับนี้เป็นตอนต่อจากฉบับก่อนหน้านี้ดังนี้
ปีที่
๒ ฉบับที่ ๑๗๔ วันอาทิตย์ที่
๒๐ มิถุนายน ๒๕๕๓ เรื่อง
"การคำนวณเชิงตัวเลข (๑) การแก้สมการอนุพันธ์ด้วยฟังก์ชันพหุนาม"
ปีที่
๒ ฉบับที่ ๑๗๕ วันจันทร์ที่
๒๑ มิถุนายน ๒๕๕๓ เรื่อง
"การคำนวณเชิงตัวเลข (๒) การแก้สมการอนุพันธ์ด้วยฟังก์ชันพหุนาม"
ปีที่
๗ ฉบับที่ ๘๙๖ วันพฤหัสบดีที่
๒๗ พฤศจิกายน ๒๕๕๗ เรื่อง
"การคำนวณเชิงตัวเลข (๕) การแก้สมการอนุพันธ์ด้วยฟังก์ชันพหุนาม"
ปีที่
๗ ฉบับที่ ๘๙๙ วันพุธที่ ๓
ธันวาคม ๒๕๕๗ เรื่อง
"การคำนวณเชิงตัวเลข (๖) การแก้สมการอนุพันธ์ด้วยฟังก์ชันพหุนาม"
ทั้ง
๔ เรื่องข้างต้นถูกนำไปรวมไว้ใน
"MO Memoir รวมบทความชุดที่ ๑๖ วิศวกรรมเคมีภาคคำนวณ"
ที่สามารถดาวน์โหลดไฟล์
pdf ได้จากหน้า
blog
ในตอนที่
๑ (ฉบับที่
๑๗๔)
และตอนที่
๒ (ฉบับที่
๑๗๕)
ของเรื่องนี้
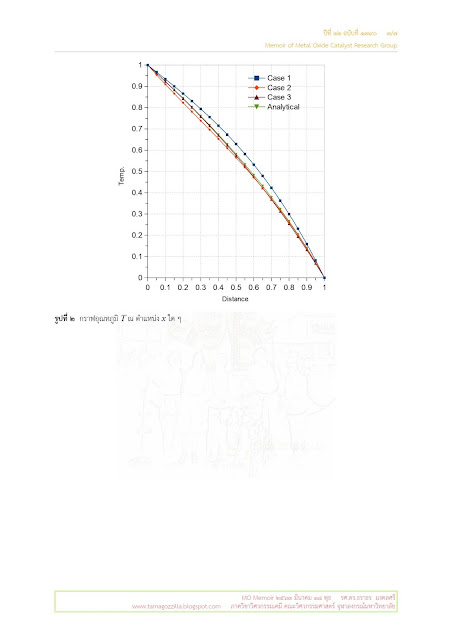
ได้แสดงให้เห็นว่าการเลือกจุดที่กำหนดให้ค่า
residual
เป็นศูนย์นั้น
(จุดที่เรียกว่า
collocation
point) ส่งผลต่อความถูกต้องของคำตอบที่ได้
แต่โดยหลักก็คือตำแหน่งของจุดที่เลือกนั้นควรเป็นบริเวณที่คำตอบมีการเปลี่ยนแปลงรวดเร็วเมื่อเทียบกับบริเวณอื่น
แต่เนื่องจากในหลายกรณีเรามักไม่รู้ว่าคำตอบที่ได้นั้นจะมีการเปลี่ยนแปลงอย่างใด
จึงได้มีการนำเสนอว่าถ้าเราประมาณคำตอบด้วย
orthogonal
polynomial จุดที่เลือกก็ควรเป็น
root
(จุดที่ค่าฟังก์ชันเป็นศูนย์)
ของ
orthogonal
polynomial และในตอนที่
๔ ของเรื่องนี้ (ฉบับที่
๘๙๙)
ก็ได้ทิ้งท้ายว่าจะหาเวลามาเขียนเรื่องนี้ต่อ
แต่ไม่รู้เหมือนกันว่าทำไมถึงลืมเรื่องนี้ไปได้
วันนี้ก็เลยขอมาเขียนต่อ
โดยขอเป็นเรื่อง "Orthogonal
function" หรือที่มีคนแปลเป็นไทยว่า
"ฟังก์ชันเชิงตั้งฉากก็แล้วกัน"
ก็แล้วกัน






ไม่มีความคิดเห็น:
แสดงความคิดเห็น