Memoir ฉบับนี้ย้อนกลับมายังความรู้สมัยป.ตรี เพื่อการใช้งานจริง สำหรับนิสิตที่กำลังจะไปฝึกงาน หรือนิสิตที่กำลังจะจบเพื่อไปทำงาน โดยฉบับนี้จะจำกัดอยู่ที่ Bernoulli's equation หรือสมการของแบร์นูลลี
สมการของแบร์นูลลีเป็นสมการอนุรักษ์พลังงานที่เราใช้กันเป็นประจำในการคำนวณการไหลของของไหล (ทั้งของเหลวและแก๊ส) ที่ไหลจากตำแหน่งหนึ่งไปยังอีกตำแหน่งหนึ่ง สำหรับของไหลที่ไม่สามารถอัดตัวได้ (incompressible fluid) เช่นของเหลวที่ใช้งานกันทั่วไปในโรงงานที่ความดันไม่ได้สูงมาก รูปแบบทั่วไปของสมการของแบร์นูลลีคือ (สมการที่ 1)
โดยที่ v คือความเร็ว h คือความสูง p คือความดัน คือความหนาแน่น และ g คือค่าคงที่เนื่องจากแรงดึงดูดของโลก ตามสมการที่ (1) นั้นทุกพจน์จะมีหน่วยเป็นพลังงาน โดยพจน์แรกเป็นตัวแทนของพลังงานจลน์ (ρv2/2) พจน์ที่สอง (ρgh) เป็นตัวแทนของพลังงานศักย์ และพจน์ที่สาม (p) เป็นตัวแทนของความดัน
สมการที่ (1) ที่ทุกพจน์มีหน่วยเป็นพลังงานนั้นทำให้มองเห็นภาพได้ยากในการใช้งาน โดยเฉพาะในการปั๊มของเหลวจากตำแหน่งหนึ่งไปยังอีกตำแหน่งหนึ่งนั้น ตัวที่เป็นปัญหามากในการคำนวณขนาดของปั๊มคือความแตกต่างของระดับความสูงระหว่างตำแหน่งต้นทางและตำแหน่งปลายทาง ดังนั้นเพื่อให้สมการมีรูปแบบที่มองเห็นภาพได้ง่ายในการใช้งาน บ่อยครั้งที่เราจะเห็นการเขียนสมการของแบร์นูลลีในรูปแบบที่ทุกพจน์มีหน่วยเป็นความสูง ดังนี้ (สมการที่ 2)
เนื่องจากงานของพวกคุณจะจำกัดอยู่ที่การไหลของของเหลวในท่อเป็นหลัก ดังนั้นใน memoir นี้จะจำกัดเนื้อหาไว้ที่การไหลของของเหลวในท่อ (ซึ่งถือว่าอัดตัวไม่ได้) ในกรณีของการไหลจากตำแหน่ง (1) ไปยังตำแหน่ง (2) และมีแรงเสียดทานในท่อ สมการที่ (1) สามารถเขียนได้ในรูป (สมการที่ 3)
สิ่งที่ต้องพึงระลึกคือสมการของแบร์นูลลีนั้น
(ก) พิจารณาระบบที่สภาวะคงตัว (steady state) เท่านั้น ไม่ได้ "คำนึง" ถึงสภาพระบบตอนเริ่มต้นเดินเครื่อง (start up) แต่ในการออกแบบทางวิศวกรรมนั้น เรา "ต้องคำนึง" ด้วยว่าเมื่อออกแบบมาแล้วจะเริ่มเดินเครื่องได้อย่างไร และ
(ข) พิจารณาเฉพาะความสูงเฉพาะตำแหน่งเริ่มต้นและตำแหน่งสุดท้าย ไม่ได้พิจารณาว่าระหว่างเส้นทางนั้นมีความสูงเปลี่ยนแปลงหรือไม่อย่างไร แต่ในการเลือกขนาดปั๊มนั้น "จำเป็น" ต้องพิจารณาด้วยว่าระหว่างเส้นทางนั้น การเปลี่ยนแปลงความสูง (ในทิศทางที่สูงกว่าตำแหน่งเริ่มต้น) ที่มีค่ามากที่สุดนั้น มีค่าเท่าใด เพราะจำเป็นสำหรับการเริ่มต้นเดินเครื่อง (เดี๋ยวจะยกตัวอย่างให้เห็น)
ตัวอย่างที่ 1 กาลักน้ำ (siphon)
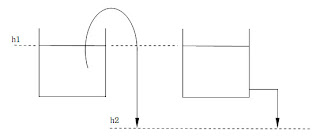
หวังว่าทุกคนคงรู้จักการลักน้ำ ทีนี้ลองพิจารณารูปที่ 1 ข้างล่างซึ่งเป็นการถ่ายน้ำออกจากถังสองใบ โดยระดับน้ำในถังทั้งสองใบอยู่ที่ระดับ h1 เท่ากัน ถังใบซ้ายใช้วิธีเอาปลายข้างหนึ่งของสายยางจุ่มลงไปในถังและปลายอีกข้างหนึ่งปล่อยให้อยู่ต่ำกว่าถังที่ระดับ h2 ส่วนถังใบขวาใช้วิธีเจาะรูด้านข้างถัง และต่อท่อให้ปลายท่ออยู่ต่ำลงมาที่ระดับ h2 เหมือนกัน ถ้าสมมุติให้แรงเสียดทานเนื่องจากการไหลในท่อมีค่าน้อยมากจนตัดทิ้งไปได้ ให้ท่านพิจารณาว่า
(ก) ลองใช้สามัญสำนึกพิจารณาว่า วิธีการแบบไหนจะทำให้มีน้ำไหลออกมาทางปลายท่อที่ระดับ h2
(ข) ถ้าคำนวณโดยใช้สมการของแบร์นูลลี วิธีการแบบไหนจะทำให้มีน้ำไหลออกมาทางปลายท่อที่ระดับ h2
รูปที่ 1 ถังน้ำทั้งสองใบมีระดับน้ำอยู่ที่ h1 เท่ากัน และปลายท่อน้ำไหลออกอยู่ที่ระดับ h2 เท่ากัน
จากการใช้สามัญสำนึก (คงมีกันนะ) คงมองออกว่าการเอาปลายข้างหนึ่งของสายยางจุ่มลงในถังน้ำ และปล่อยให้ปลายอีกข้างหนึ่งอยู่ต่ำกว่าระดับน้ำในถังน้ำนั้น "ไม่สามารถ" ทำให้น้ำไหลออกมาจากถังน้ำตามสายยางได้ (ซึ่งตรงกับความเป็นจริง) แต่ถ้าใช้วิธีการเจาะรูทางด้านข้างถังจะมีน้ำไหลออกมาได้ (ซึ่งก็ตรงกับความเป็นจริงอีก)
แต่ถ้าใช้สมการของแบร์นูลลี (ตามสมการที่ 3) ถ้าขนาดพื้นที่หน้าตัดของถังนั้นใหญ่มากเมื่อเทียบกับพื้นที่หน้าตัดของสายยาง ที่ระดับ h1 จะพอประมาณได้ว่าความเร็ว v1 มีค่าเป็น 0 p1 เท่ากับ p2 คือความดันบรรยากาศ และทั้งสองวิธีจะมีน้ำไหลออกมาทางปลายท่อที่ระดับ h2 ได้ ซึ่งไม่ตรงกับความเป็นจริงในกรณีของรูปด้านซ้าย
แล้วการใช้สมการของแบร์นูลลีผิดพลาดตรงไหน
ในการทำกาลักน้ำนั้น เราจะต้อง "เติม" น้ำให้เต็มในสายยางก่อน จากนั้นจึงใช้นิ้วอุดปลายสายยางทั้งสองข้างก่อนที่จะจุ่มปลายข้างหนึ่งลงในถัง และปล่อยให้ปลายอีกข้างหนึ่งอยู่ต่ำกว่าระดับน้ำในถัง เมื่อเราเปิดนิ้วที่อุดรูสายยางอยู่ก็จะทำให้น้ำไหลออกมาจากท่อ ทำให้ความดันในสายยางลดต่ำกว่าความดันบรรยากาศ ความดันบรรยากาศก็จะดันให้น้ำในถังไหลเข้าไปในสายยาง สูงขึ้นไปเหนือระดับปากถัง (ซึ่งอยู่สูงกว่าระดับ h1) และไหลตกลงมาทางปลายด้าน h2 ทำให้น้ำไหลได้อย่างต่อเนื่อง (ซึ่งขณะนี้สมการของแบร์นูลลีใช้ได้แล้ว) จะเห็นว่าเส้นทางการไหลของน้ำนั้นมีการไหลไปยังระดับที่สูงกว่าระดับเริ่มต้น (น้ำไหลเองจากที่ต่ำไปยังที่สูงไม่ได้) ซึ่งช่วงนี้การไหลต้องการพลังงานเพื่อที่จะไหลขึ้นไปได้ โดยพลังงานดังกล่าวจะได้กลับคืนมาในช่วงที่ไหลลง
แต่ถ้าเป็นแบบทางรูปด้านขวานั้น น้ำไม่มีเส้นทางการไหลขึ้นไปสูงกว่าระดับที่สูงที่สุดของน้ำ (h1) ทำให้เมื่อเจาะรูที่ข้างถังน้ำ น้ำก็สามารถไหลออกมาได้ทันที
ตัวอย่างที่ 2 การถ่ายเทของเหลวจากถังทางด้านซ้ายไปยังถังทางด้านขวา
พิจารณาการถ่ายเทของเหลวจากถังทางด้านซ้ายไปยังถังทางด้านขวาที่แสดงในรูปที่ 2 เนื่องจากระหว่างถังทั้งสองมีถนนคั่นกลางอยู่ ดังนั้นวิศวกรจึงวางแผนที่จะเดินท่อแบบ
(ก) ยกสูงข้ามถนน (ตามแนวเส้นสีเขียว) หรือ
(ข) ทำทางลอดใต้ถนน (ตามแนวเส้นสีน้ำเงิน)
คำถามคือทั้งสองวิธีการนั้น (ถ้าค่าการสูญเสียเนื่องจากแรงเสียดทานในท่อนั้นเท่ากัน) จะใช้ปั๊มที่มีขนาดเท่ากันหรือแตกต่างกันอย่างไร
รูปที่ 2 การถ่ายของเหลวโดยใช้ปั๊มสูบของเหลวจากถังทางด้านซ้ายไปยังถังทางด้านขวา h1 คือระดับความสูงของของเหลวในถังด้านซ้าย h2 คือระดับความสูงของของเหลวในถังด้านขวา h3 คือระดับความสูงของถังทั้งสอง (h3 > h2 และ h3 > h1 แต่ h1 และ h2 เปลี่ยนแปลงระดับตลอดเวลาที่ทำการสูบของเหลว) h4 คือระดับความสูงของท่อถ้าหากต้องการยกสูงข้ามถนน (h4 > h3) และ h5 คือระดับความลึกของท่อที่ต้องการเดินลอดถนน ความสูงของตำแหน่งปั๊มให้ถือว่าอยู่ที่ระดับพื้นดิน
ลองเริ่มจากการสมมุติว่าเราไม่มีปั๊ม และระดับน้ำในถังด้านซ้าย (h1) สูงกว่าระดับน้ำในถังด้านขวา (h2) ถ้าเราเอาสมการของแบร์นูลลีมาจับ จะพบว่าสมการของแบร์นูลลีจะบอกว่ามีน้ำไหลจากถังด้านซ้ายไปยังถังด้านขวาได้ไม่ว่าจะเดินท่อยกสูงข้ามถนนหรือลอดใต้พื้นถนน
แต่ถ้าเอาความเป็นจริงมาจับคุณคงจะบอกได้ว่าจะมีน้ำไหลจากถังด้านซ้ายไปยังถังด้านขวาได้เฉพาะในกรณีที่เดินท่อลอดใต้ถนนเท่านั้น ส่วนการเดินท่อยกข้ามถนนไปนั้นจะไม่มีน้ำไหลไปอีกฝั่ง เพราะน้ำไม่สามารถไหลได้เองจากระดับ h1 ขึ้นไปยังระดับท่อที่อยู่เหนือถนน h4 ที่อยู่สูงกว่าได้ แต่ถ้าหากคุณทำให้น้ำไหลขึ้นไปยังระดับ h4 และไหลลงมาอีกทางฝั่งได้ น้ำก็จะไหลต่อเนื่องได้เอง (เหมือนกับกาลักน้ำในตัวอย่างที่ 1)
ในการเลือกขนาดปั๊มนั้น ถ้าคุณใช้สมการของแบร์นูลลีเพียงอย่างเดียว คุณจะได้ปั๊มที่มีเฮดเท่ากับ (ความสูงของถัง + อัตราการไหลที่ต้องการ + แรงเสียดทานในท่อ) ซึ่งค่าเฮดที่ได้นั้นจะไม่มีปัญหาใดถ้าหากคุณเดินท่อ "ลอด" ใต้พื้นถนน แต่ถ้าเป็นการเดินท่อยกสูง "ข้าม" ถนนแล้วล่ะก็ ถ้าค่าเฮดที่คำนวณได้นี้น้อยกว่าค่า h4 ปั๊มของคุณจะไม่มีวันสูบของเหลวข้ามไปยังอีกฟากหนึ่งได้
ดังนั้นในการออกแบบระบบท่อที่สูบของเหลวจากที่หนึ่งไปยังอีกที่หนึ่งนั้น คุณสามารถประมาณได้ว่าขนาดเฮดที่น้อยที่สุดที่ปั๊มจะต้องทำได้คือระยะความสูงที่สูงจากตัวปั๊มมากที่สุด ไม่เช่นนั้นระบบของคุณจะไม่สามารถผลักดันของเหลวให้ไหลไปยังอีกฟากหนึ่งได้
ตัวอย่างที่ 2 นี้แสดงให้เห็นว่าการเลือกขนาดปั๊มนั้นไม่ใช่ดูเฉพาะความสูงที่ตำแหน่งต้นทางกับปลายทาง แต่ต้องพิจารณาความสูงในระหว่างกลางประกอบด้วย
ตัวอย่างที่ 3 แบบไหนน้ำไหลแรงกว่ากัน
พิจารณาการไหลของน้ำออกจากถังออกทางท่อผ่านวาล์วควบคุมอัตราการไหลที่แสดงในรูปที่ 3 ข้างล่าง (โจทย์ข้อนี้ดัดแปลงมาจากปัญหาการติดตั้งวาล์วในการดึงผลิตภัณฑ์ที่เป็นของเหลวออกทางด้านข้างหอกลั่น)
คำถามมีอยู่ว่า ที่ปลายท่อที่ระดับ h4 นั้น น้ำไหลออกมาแรงเท่ากันหรือไม่ (ให้แรงเสียดทานเนื่องจากการไหลในสองระบบนั้นเท่ากัน)
รูปที่ 3 ตำแหน่งการติดตั้งวาล์วควบคุมอัตราการไหล h1 คือระดับผิวบนของน้ำในถัง h2 และ h3 คือระดับตำแหน่งที่ติดตั้งวาล์ว (h2 อยู่สูงกว่า h3) และ h4 คือระดับปลายด้านขาออกของท่อ
ถ้าเอาสมการของแบร์นูลลีมาจับกับระบบทั้งสอง (โดยไม่ได้ดูความเป็นจริงว่าโครงสร้างของระบบเป็นอย่างไร) ก็จะพบว่าความเร็วในการไหลของน้ำในทั้งสองระบบจะขึ้นอยู่กับความแตกต่างของความสูง (h1 - h4) แต่ถ้าใช้สามัญสำนึกพิจารณา คุณก็คงจะรู้สึกว่าระบบทางด้านขวานั้นควรจะให้น้ำไหลแรงกว่าระบบทางด้านซ้าย ซึ่งมันขัดกับสิ่งที่สมการของแบร์นูลลีทำนายไว้ แล้วความผิดพลาดมันอยู่ตรงไหนล่ะ
เวลาที่เราเรียนสมการของแบร์นูลลีนั้น มีข้อสมมุติข้อหนึ่งที่หายไปจากการเรียนคือ มีของเหลวไหลอยู่เต็มพื้นที่หน้าตัดของท่อทั้งสองฝากฝั่งของวาล์ว ในกรณีที่ความต้านทานที่จุดใดจุดหนึ่งของระบบท่อสูงกว่าความต้านทานในส่วน downstream ของตำแหน่งนั้นลงไป จุดนั้นจะเป็นจุดกำหนดอัตราเร็วที่ของไหลนั้นจะเคลื่อนผ่านไปได้
กรณีรูปด้านซ้ายของรูปที่ 3 นั้น ความต้านทานส่วนใหญ่ของระบบจะอยู่ที่ตัววาล์ว ถ้าวาล์วเปิดไม่มาก (หรือเปิดเต็มที่ แต่ตัววาล์ว (เช่น globe valve) เองก็มีความต้านทานสูงกว่าระบบท่อในช่วงถัดไป) อัตราการไหลของน้ำที่ไหลผ่านวาล์วจะขึ้นอยู่กับความแตกต่างของระดับความสูง (h1 - h2) แต่ในกรณีของรูปด้านขวานั้น อัตราการไหลของน้ำที่ไหลผ่านวาล์วจะขึ้นอยู่กับความแตกต่างของระดับความสูง (h1 - h3) ซึ่งมีค่ามากกว่าของกรณีรูปด้านซ้าย
เรื่องตำแหน่งติดตั้งวาล์วและการวางระบบท่อนั้นยังมีเรื่องเล่าจากประสบการณ์ให้ฟังอีกหลายเรื่อง ส่วนใหญ่เป็นเรื่องที่ไม่มีเขียนเอาไว้ในตำรา แต่สามารถนำเอาความรู้ที่เรียนมานั้นมาประยุกต์ใช้อธิบายได้ เอาไว้ค่อย ๆ เล่าให้ฟังเป็นระยะไปก็แล้วกัน
หมายเหตุ : ในโรงงานที่ตั้งกลางแจ้งเช่นพวกโรงกลั่นน้ำมันหรือโรงปิโตรเคมีนั้น ความกว้างของถนนและความสูงของท่อต่าง ๆ ที่ยกข้ามถนนต้องนำเอาขนาดของเครื่องจักรกลต่าง ๆ ที่ต้องใช้ในการก่อสร้างและซ่อมบำรุงเข้ามาพิจารณาด้วย เช่นขนาดรถเครน ซึ่งต้องรู้ความสูงและวงเลี้ยวที่รถต้องใช้เวลาเคลื่อนย้าย สำหรับเส้นทางสัญจรทั่วไปนั้นเรามักจะเห็นป้ายบอกว่า สะพานลอยหรือสายไฟฟ้าต่าง ๆ ที่พาดข้ามถนนมักจะสูงจากพื้นถนนอย่างน้อย 5 เมตร (ระยะความสูงมาตรฐาน)
ในกรณีที่รถบรรทุกนั้นเมื่อบรรทุกอุปกรณ์แล้วมีความสูงเกิน 5 เมตร ถ้าเกินไปมากก็ต้องทำเรื่องวางแผนขออนุญาตยกสะพานลอยออกชั่วคราว (สะพานให้คนข้ามนะ มันยกออกได้ แต่ถ้าเป็นสะพานให้รถข้าม มันยกไม่ได้) และยก (หรือบางครั้งต้องตัดแล้วต่อใหม่) สายไฟที่พาดผ่านออกชั่วคราว
สมัยก่อนที่ยังทำงานอยู่ทางภาคตะวันออก เวลาที่อุปกรณ์ที่มีขนาดใหญ่มากที่ส่งมาจากต่างประเทศต้องระบุให้เรือมาเทียบท่าที่ท่าเรือสัตหีบ (ตอนนั้นยังไม่มีท่าเรือแหลมฉบัง) เพราะถ้าไปที่คลองเตยเมื่อใดจะมีปัญหาไม่สามารถขนย้ายอุปกรณ์ออกจากท่าเรือและเคลื่อนที่ผ่านถนนออกมายังถนนบางนา-ตราดได้ เพราะมันมีสิ่งกีดขวางสารพัดอย่าง แต่ถึงกระนั้นก็เคยมีรายกายปิดถนนสุขุมวิทช่วงจากท่าเรือสัตหีบมายังทางเข้านิคมอุตสาหกรรม (สมัยนั้นเป็นทางลาดยางเล็ก ๆ แค่ 2 ช่องทางจราจร ไหล่ทางยังเป็นหินอยู่เลย ไม่ได้ลาดยางด้วย) เพื่อขนเครื่องปฏิกรณ์ขนาดใหญ่มาตามถนน
ทางฝ่ายผู้ควบคุมการขนส่งไม่เพียงแต่ต้องตรวจสอบเส้นทางว่ามีอะไรขวางอยู่ด้านบน แต่ยังต้องตรวจสอบความแข็งแรงของสะพานที่จะนำรถบรรทุกหนักเคลื่อนที่ผ่านด้วย สำหรับพื้นถนนนั้น การเพิ่มจำนวนล้อจะเป็นการกระจายแรงกดบนพื้นถนน แรงกดของแต่ละล้อบนพื้นถนนก็จะลดลง ป้องกันความเสียหายแก่พื้นถนนได้ ดังนั้นถ้าบรรทุกหนักมากก็เพิ่มจำนวนล้อให้มากขึ้น แต่ในกรณีของสะพานนั้นน้ำหนักทั้งหมดของตัวรถจะถ่ายลงไปที่ระบบคานและเสา (ไม่ได้กระจายไปตามพื้นดินเหมือนวิ่งบนถนน) การเพิ่มจำนวนล้อไม่ได้ช่วยอะไรในการลดน้ำหนักที่สะพานต้องรองรับ
ไม่มีความคิดเห็น:
แสดงความคิดเห็น