เก็บตกงานก่อสร้างถังเก็บน้ำสำรอง MO Memoir : Friday 12 December 2557

บางที่วิธีการที่จะทำให้รู้ว่าสิ่งที่ออกแบบมานั้นใช้งานได้จริงหรือไม่ก็คือ "การทดลองลงมือใช้งาน" ภายใต้สถานการณ์สมมุติที่แตกต่างกัน โดยอาจเริ่มตั้งแต่ การเริ่มเดินเครื่องเป็นครั้งแรก การปฏิบัติงานในระหว่างการเดินเครื่องตามปรกติ การแก้ปัญหาถ้าหากเกิดปัญหาในระหว่างการเดินเครื่อง การหยุดเดินเครื่อง และการซ่อมบำรุง
  

มีอยู่ไม่น้อยที่พบว่าในระหว่างการก่อสร้างและติดตั้งอุปกรณ์นั้น ไม่มีปัญหาใด ๆ ในการติดตั้งอุปกรณ์ชิ้นนั้น เพราะมีทั้งรถเครน (สำหรับการยกของขึ้นที่สูงหรือยกของหนัก) และนั่งร้าน (สำหรับการปฏิบัติงานในที่สูง) แต่พอเสร็จสิ้นงานก่อสร้าง นั่งร้านก็จะถูกรื้อทิ้ง รถเครนถูกนำออกไปจากพื้นที่ฝ่ายผลิต และเมื่อถึงเวลาที่ต้องเริ่มเดินเครื่องจริง (หรือเมื่อถึงคราวต้องหยุดเดินเครื่องเพื่อทำการซ่อมบำรุง) ปัญหาจะปรากฏให้เห็น อย่างเช่นกรณีของถังเก็บน้ำสำรองที่ยกมาเป็นตัวอย่างให้ดูในวันนี้
  

รูปที่ ๑ วาล์วควบคุมการไหลของน้ำประปาเข้าถังเก็บติดตั้งอยู่ทางด้านบนของถัง (ในกรอบสีเหลือง)

  

ถังเก็บน้ำในรูปสูงเกือบ ๑๐ เมตรจากพื้น ท่อน้ำเข้าถังต่อตรงจากท่อน้ำประปาโดยจ่ายเข้าทางด้านบนของถัง (แบบเดียวกับถังเก็บน้ำที่ใช้กันตามบ้านทั่วไป) ตรงจุดท่อน้ำเข้าถังจะมีวาล์วปีกผีเสื้อติดตั้งอยู่ (ที่อยู่ในกรอบสีเหลืองในรูปที่ ๑) จากนั้นปั๊มน้ำจะทำการสูบน้ำจากในถังเพื่อจ่ายไปยังส่วนต่าง ๆ ของโรงงานอีกที ถึงจุดนี้พอจะสังเกตเห็นอะไรบ้างไหมครับ
  

สิ่งที่เห็นได้ในรูปที่ ๑ และ ๒ ตำแหน่งที่ติดตั้งวาล์วเปิด-ปิดน้ำเข้าถังนั้น ไม่มีพื้นที่ให้ผู้ปฏิบัติงานยืนทำงานเพื่อทำการเปิด-ปิดวาล์ว และเป็นตำแหน่งที่อยู่สูงจากพื้นมาก รูปที่ถ่ายมานี้อยู่ในช่วงระหว่างการทดสอบระบบ ดังนั้นจึงมีการติดตั้งนั่งร้านชั่วคราวเพื่อทำการเปิด-ปิดวาล์ว แต่ท้ายสุดแล้วนั่งร้านชั่วคราวดังกล่าวจะถูกรื้อออกและวาล์วทุกตัวจะเปิดทิ้งไว้ (เข้าใจว่าระดับน้ำในถังจะคุมด้วยลูกลอย เหมือนกับถังเก็บน้ำประปาที่ใช้กันตามบ้านทั่วไป)
  

ถ้าเป็นวาล์วที่นาน ๆ ทีใช้งานครั้งนึง หรือเป็นวาล์วที่ไม่อยากให้ใครเข้าไปยุ่งอะไรกับมันโดยไม่จำเป็น การติดตั้งแบบนี้บ่อยครั้งก็ถือว่าเป็นที่ยอมรับ การตั้งนั่งร้านชั่วคราวเพื่อการใช้งานนาน ๆ ครั้งอาจจะดีกว่าการมีโครงสร้างถาวรที่นาน ๆ ครั้งจะมีการใช้งานสักที และการที่ปิดช่องทางให้คนเข้าไปยุ่งอะไรกับมันได้ง่าย ๆ (ด้วยการให้มันอยู่สูงเกินเอื้อม) ก็อาจถือได้ว่าเป็นความปลอดภัยอย่างหนึ่งสำหรับวาล์วที่ต้องการให้มันคงอยู่ ณ ตำแหน่งใดตำแหน่งหนึ่ง (คือเปิดค้างหรือปิดค้าง) โดยไม่ต้องการให้ใครเข้าไปยุ่งอะไรกับมันเว้นแต่จะมีการกำหนดการทำงานที่ชัดเจนว่าให้ไปยุ่งอะไรกับมันเท่านั้น ซึ่งตรงนี้ก็ต้องไปดูกันที่คู่มือการปฏิบัติงาน (operating manual) ของโรงงานว่าวาล์วดังกล่าวมีความถี่ในการใช้งานมากน้อยเท่าใด
  

รูปที่ ๒ ภาพขยายกรอบสีเหลืองในรูปที่ ๑

ถังน้ำที่ใช้เก็บน้ำประปากันตามบ้านเรือนต่าง ๆ เราจะเปิดวาล์วที่ให้น้ำประปาไหลเข้าถังทิ้งไว้ตลอด แต่ใช้ลูกลอยคุมระดับน้ำไม่ให้ล้นถังเก็บอีกทีเวลาที่น้ำเต็มถัง โดยลูกลอยดังกล่าวติดตั้งอยู่ในตัวถังน้ำ ซึ่งในกรณีของถังเก็บที่นำมาแสดงนี้ก็เดาว่าเป็นแบบเดียวกัน แต่ในที่นี้มันมีเรื่องหนึ่งงที่ควรต้องนำมาพิจารณาประกอบคือ ความถี่ของการที่ลูกลอยมีโอกาสที่จะเสียและความถี่ในการตรวจสอบการทำงานและการถอดซ่อมบำรุงลูกลอยเข้ามาพิจารณาด้วย เพราะลูกลอยมีโอกาสที่จะ “ค้าง” ได้โดยที่เราไม่ต้องการ (คือไม่ลอยขึ้นเพื่อปิดการไหลของน้ำ หรือไม่ตกลงเพื่อเปิดให้น้ำไหล)
  

ตรงนี้เป็นประเด็นที่ควรต้องหารือกันระหว่าง ผู้ออกแบบ ผู้จ่ายเงิน และผู้ปฏิบัติงาน สิ่งที่ผู้ออกแบบคาดหวังก็คือสิ่งที่ออกแบบไว้นั้นสามารถปฏิบัติงานได้จริง ในขณะที่ผู้จ่ายเงินนั้นต้องการค่าใช้จ่ายที่ต่ำที่สุด ส่วนผู้ปฏิบัติงานนั้นต้องการการทำงานที่สะดวกสบายที่สุด ซึ่งความต้องการของคนสามกลุ่มนี้อาจจะไม่เหมือนกันพร้อม ๆ กัน
  

ตัวอย่างเช่นในกรณีนี้ผู้ออกแบบอาจจะออกแบบให้มี platform ถาวรติดตั้งอยู่บนยอดถัง เพื่อให้ความสะดวกแก่ผู้ปฏิบัติงานในการทำงาน ซึ่งผู้ปฏิบัติงานก็เห็นชอบด้วย แต่ผู้จ่ายเงิน (ซึ่งไม่ใช่คนที่ต้องลงมาทำงานดังกล่าวในการใช้งานจริง) อาจพิจารณาว่าการติดตั้ง platform ดังกล่าวจะทำให้ค่าใช้จ่ายเพิ่มสูงขึ้น และวาล์ว/ลูกลอยดังกล่าวก็ไม่ได้มีการใช้งานบ่อยครั้ง ดังนั้นการติดตั้งนั่งร้านชั่วคราวเมื่อต้องการขึ้นไปปฏิบัติงานยังตำแหน่งดังกล่าวจึงอาจเป็นการเหมาะสมกว่า (ในแง่ของค่าใช้จ่ายที่ไม่ต้องจ่ายให้กับโครงสร้างที่นาน ๆ ครั้งจะมีการใช้งาน)

อีกเรื่องหนึ่งที่ควรต้องนำมาพิจารณาคือตำแหน่งทางเข้าของน้ำว่าในกรณีนี้ทำไมจึงให้เข้าทาง “ด้านบน”
  

ความดันของของเหลวนั้นขึ้นอยู่กับ “ความสูง” เท่านั้นเท่านั้น ไม่ขึ้นกับพื้นที่หน้าตัดของภาชนะเก็บของเหลว เรื่องนี้เคยกล่าวไว้ครั้งหนึ่งแล้วใน Memoir ปีที่ ๕ ฉบับที่ ๕๘๙ วันศุกร์ที่ ๑๕ มีนาคม ๒๕๕๖ เรื่อง “ความรู้เบื้องต้นเกี่ยวกับปั๊มตอนที่ ๑”
  

ในโรงงานทั่วเช่นโรงกลั่นน้ำมัน การสูบน้ำมันเข้าแทงค์นั้นจะสูบเข้าทาง “ก้นแทงค์” เพราะจะทำให้ปั๊มกินพลังงานเฉลี่ยน้อยที่สุด เพราะแรงต้านด้านขาออก (เนื่องจากความสูงของของเหลว) จะค่อย ๆ เพิ่มสูงขึ้นตามระดับความสูงของของเหลวในแทงค์ แต่ถ้าสูบเข้าทางด้านบน ปั๊มจะต้องทำงานหนักตลอดเวลา เพราะแรงต้านด้านขาออกจะสูงคงที่ตลอด เวลา (เท่ากับระดับความสูงของท่อด้านขาออกที่จ่ายเข้าทางด้านบนของแทงค์ แต่ทั้งนี้ก็ต้องพิจารณาด้วยนะว่าปลายท่อด้านที่อยู่ในถังนั้นมันอยู่ที่ระดับไหน ถ้าปลายท่อด้านที่อยู่ในถังมันต่ำกว่าระดับสูงสุดของท่อด้านขาออก ปั๊มก็ยังต้องสามารถส่งของเหลวขึ้นไปได้สูงที่ระดับความสูงนั้นก่อน พอของเหลวเริ่มไหลตกลงมาทางท่อด้านขาออก พลังงานที่ปั๊มต้องใช้ก็จะลดลงเอง (นึกภาพกาลักน้ำดูนะ) เรื่องนี้เคยเล่าเอาไว้แล้วใน Memoir ปีที่ ๔ ฉบับที่ ๔๕๖ วันจันทร์ที่ ๒๘ พฤษภาคม ๒๕๕๕ เรื่อง “เก็บตกฝึกงานฤดูร้อน ๒๕๕๕”
  

แต่ก็ไม่ใช่ว่าจะไม่มีการสูบเข้าทางด้านบนนะ มันก็มีเหมือนกันในกรณีของการที่ต้องการผสมของเหลวในแทงค์ โดยสูบออกทางด้านล่างและป้อนกลับเข้ามาใหม่ทางด้านบน

รูปที่ ๓ การสูบของเหลวเข้าถังเก็บโดย (ก) เข้าทางด้านก้นถัง (ข) เข้าทางด้านบน (ค) เข้าทางด้านบนแต่ท่อด้านในวกลงล่าง

รูปที่ ๓ ข้างบนเป็นตัวอย่างการต่อท่อจากปั๊มเข้าถังเก็บรูปแบบต่าง ๆ การต่อท่อเข้าที่ก้นถังตามรูปแบบ (ก) นั้น แรงด้านด้านขาออกของปั๊มจะค่อย ๆ เพิ่มตามระดับความสูงของของเหลวในถัง (h1) ดังนั้นถ้าเป็นช่วงที่ระดับของเหลวต่ำ ปั๊มจะมีแรงต้านด้านขาออกน้อยและจะกินพลังงานน้อย เมื่อระดับของเหลวในถังเพิ่มสูง แรงต้านด้านขาออกก็จะเพิ่มขึ้น ดังนั้นปั๊มก็จะกินพลังงานเพิ่มมากขึ้นตามระดับความสูงของของเหลวในถัง (h1)
  

รูปแบบ (ข) เป็นกรณีของการต่อท่อเข้าด้านบนของถัง ในกรณีนี้แรงต้านด้านขาออกจะเท่ากับระดับความสูงของท่อด้านขาออกคือ h2 ตลอดเวลาโดยไม่ขึ้นกับระดับความสูงของของเหลวในถัง (h1) ดังนั้นปั๊มจะกินพลังงานเต็มที่ตลอดเวลาไม่ว่าของเหลวในถังจะมีปริมาณเท่าใด
  

ส่วนรูปแบบ (ค) นั้นปั๊มจำเป็นต้องมีพลังงานมากพอที่จะดันของเหลวให้สูงขึ้นไปจนถึงระดับ h2 (ตำแหน่งสูงสุดของท่อให้ได้ก่อน) จากนั้นเมื่อของเหลวเริ่มไหลตกลงมาทางปลายท่อ (ของเหลวต้องไหลเต็มท่อนะ) แรงต้านด้านขาออกจะลดลงโดยเหลือเพียงแค่ระดับความสูง h3 เท่านั้น ดังนั้นตราบเท่าที่ระดับของเหลวในถังอยู่ต่ำกว่าระดับปลายท่อด้านขาอก (h3) แรงต้านด้านขาออกก็จะคงที่เท่ากับระดับความสูง h3 ตลอดเวลา และเมื่อปลายท่อด้านขาออกเริ่มจมลงในผิวของเหลว แรงต้านด้านขาออกก็จะเพิ่มตามระดับความสูงของของเหลวในถัง (h1) ในกรณีนี้ระดับความสูง h2 จะเป็นตัวกำหนดความดันด้านขาออกที่ต่ำที่สุดที่ปั๊มจำเป็นต้องมี ไม่เช่นนั้นจะไม่สามารถเริ่มการสูบของเหลวเข้าถังได้

กรณีของรูปที่ ๑ นั้นแตกต่างไปจากกรณีของรูปที่ ๓ ตรงที่กรณีของรูปที่ ๑ นั้นเป็นการต่อ “น้ำประปา” จากมิเตอร์เข้าสู่ถังเก็บโดยตรงโดยไม่มีปั๊มส่งเข้า (อาศัยแรงดันน้ำประปาที่การประปาจ่ายให้มาเพียงอย่างเดียว) ซึ่งก็เป็นรูปแบบที่ใช้กันตามบ้านทั่วไปที่จะต่อท่อน้ำประปาเข้าทางด้านบนของถังเก็บ ก่อนที่จะใช้ปั๊มสูบน้ำในถังจ่ายเข้าไปในอาคาร แต่ถังน้ำในบ้านมันมีความสูงไม่มาก (อย่างมากก็ประมาณ ๒ เมตร) ความดันในท่อประปาก็เพียงพอที่จะทำให้น้ำไหลเข้าทางด้านบนของถังได้ไม่ว่าจะเป็นเวลาไหนของวันอยู่แล้ว การต่อท่อน้ำประปาเข้าทางด้านบนของถังก็มีข้อดีตรงที่ไม่ต้องกังวลเรื่องการไหลย้อนกลับเวลาที่ความดันในท่อประปาลดต่ำลง ทำให้ไม่ต้องมีการติดตั้งวาล์วกันการไหลย้อนกลับ (non-return valve หรือcheck valve) เอาไว้เหมือนในกรณีที่ต่อท่อเข้าทางด้านก้นถัง
  

แต่ปัญหาก็คือถังในรูปที่ ๑ มันมีความสูงมาก (ประมาณ ๑๐ เมตรหรือบ้าน ๓ ชั้น) ดังนั้นจึงเกิดปัญหาว่าเวลาที่มีผู้ใช้น้ำประปามาก (เช่นในช่วงเวลากลางวัน เช้าหรือเย็น) ความดันในระบบท่อประปาจะลดต่ำลง ทำให้น้ำไม่สามารถไหลเข้าไปในถังได้ แนวทางการแก้ปัญหาที่อาจกระทำได้ก็คือทำการย้ายท่อน้ำเข้าให้มาอยู่ทางด้านก้นถังแทน (แต่ต้องมีการติดตั้งวาล์วกันการไหลย้อนกลับด้วย) หรือไม่ก็ติดตั้งถังเก็บน้ำใบเล็กกับปั๊มน้ำเพิ่มเติม โดยให้น้ำประปาไหลเข้าถังเก็บน้ำใบเล็ก (ที่มีความสูงต่ำกว่า) ก่อน จากนั้นจึงค่อยใช้ปั๊มสูบน้ำจากถังใบเล็กเข้าไปในถังใบใหญ่อีกทีหนึ่ง (รูปที่ ๔)

 

รูปที่ ๔ แนวทางหนึ่งในการแก้ปัญหา

 

ส่วนที่ว่าทำไปถึงมีปัญหานี้เกิดขึ้นมันมีเรื่องอะไรต่อมิอะไรซ้อนกันอยู่หลายอย่าง ประเด็นหนึ่งที่พอจะเอ่ยได้ก็คือคนออกแบบนั้นเป็นวิศวกรจากต่างประเทศ ไม่มีความเข้าใจในเรื่องระบบสาธารณูปโภคพื้นฐานของไทยที่แตกต่างไปจากประเทศที่เขาอาศัยอยู่ ทำให้การออกแบบที่อิงบนการใช้งาน ณ ประเทศหนึ่งไม่สามารถนำมาใช้งานได้อย่างเหมาะสมในอีกประเทศหนึ่งได้

ฝึกงานภาคฤดูร้อน ๒๕๕๓ ตอนที่ ๔ Bernoulli's equation MO Memoir : Monday 8 February 2553

Memoir ฉบับนี้ย้อนกลับมายังความรู้สมัยป.ตรี เพื่อการใช้งานจริง สำหรับนิสิตที่กำลังจะไปฝึกงาน หรือนิสิตที่กำลังจะจบเพื่อไปทำงาน โดยฉบับนี้จะจำกัดอยู่ที่ Bernoulli's equation หรือสมการของแบร์นูลลี

สมการของแบร์นูลลีเป็นสมการอนุรักษ์พลังงานที่เราใช้กันเป็นประจำในการคำนวณการไหลของของไหล (ทั้งของเหลวและแก๊ส) ที่ไหลจากตำแหน่งหนึ่งไปยังอีกตำแหน่งหนึ่ง สำหรับของไหลที่ไม่สามารถอัดตัวได้ (incompressible fluid) เช่นของเหลวที่ใช้งานกันทั่วไปในโรงงานที่ความดันไม่ได้สูงมาก รูปแบบทั่วไปของสมการของแบร์นูลลีคือ (สมการที่ 1)

โดยที่ v คือความเร็ว h คือความสูง p คือความดัน คือความหนาแน่น และ g คือค่าคงที่เนื่องจากแรงดึงดูดของโลก ตามสมการที่ (1) นั้นทุกพจน์จะมีหน่วยเป็นพลังงาน โดยพจน์แรกเป็นตัวแทนของพลังงานจลน์ (ρv²/2) พจน์ที่สอง (ρgh) เป็นตัวแทนของพลังงานศักย์ และพจน์ที่สาม (p) เป็นตัวแทนของความดัน

สมการที่ (1) ที่ทุกพจน์มีหน่วยเป็นพลังงานนั้นทำให้มองเห็นภาพได้ยากในการใช้งาน โดยเฉพาะในการปั๊มของเหลวจากตำแหน่งหนึ่งไปยังอีกตำแหน่งหนึ่งนั้น ตัวที่เป็นปัญหามากในการคำนวณขนาดของปั๊มคือความแตกต่างของระดับความสูงระหว่างตำแหน่งต้นทางและตำแหน่งปลายทาง ดังนั้นเพื่อให้สมการมีรูปแบบที่มองเห็นภาพได้ง่ายในการใช้งาน บ่อยครั้งที่เราจะเห็นการเขียนสมการของแบร์นูลลีในรูปแบบที่ทุกพจน์มีหน่วยเป็นความสูง ดังนี้ (สมการที่ 2)

เมื่อคุณได้เห็น pump curve (จะเล่าเป็นเรื่องต่อไป) คุณจะเห็นว่าแทนที่เขาจะบอกว่าปั๊มตัวนี้สร้างแรงดันขาออกได้เท่าใด เขากลับบอกว่าปั๊มตัวนี้ปั๊มน้ำขึ้นไปได้สูงกี่เมตร (ที่พูดกันว่า "เฮด" สูงกี่เมตร) เพราะการใช้หน่วยความสูงมันมองเห็นภาพชัดกว่าเวลาใช้งาน เช่นบอกว่าปั๊มตัวนี้ปั๊มน้ำขึ้นไปได้สูง 10 เมตร (ก็เพียงพอกับอาคาร 3 ชั้น) ช่างก่อสร้างหรือแรงงานทั่วไปจะมองภาพชัดเจน ไม่เหมือนกับบอกว่าปั๊มตัวนี้ทำความดันได้ 1 บรรยากาศ

เนื่องจากงานของพวกคุณจะจำกัดอยู่ที่การไหลของของเหลวในท่อเป็นหลัก ดังนั้นใน memoir นี้จะจำกัดเนื้อหาไว้ที่การไหลของของเหลวในท่อ (ซึ่งถือว่าอัดตัวไม่ได้) ในกรณีของการไหลจากตำแหน่ง (1) ไปยังตำแหน่ง (2) และมีแรงเสียดทานในท่อ สมการที่ (1) สามารถเขียนได้ในรูป (สมการที่ 3)

เมื่อตัวห้อย (1) แทนตำแหน่งเริ่มต้น และตัวห้อย (2) แทนตำแหน่งสุดท้าย และ f แทนการสูญเสียเนื่องจากแรงเสียดทานของการไหล

สิ่งที่ต้องพึงระลึกคือสมการของแบร์นูลลีนั้น

(ก) พิจารณาระบบที่สภาวะคงตัว (steady state) เท่านั้น ไม่ได้ "คำนึง" ถึงสภาพระบบตอนเริ่มต้นเดินเครื่อง (start up) แต่ในการออกแบบทางวิศวกรรมนั้น เรา "ต้องคำนึง" ด้วยว่าเมื่อออกแบบมาแล้วจะเริ่มเดินเครื่องได้อย่างไร และ

(ข) พิจารณาเฉพาะความสูงเฉพาะตำแหน่งเริ่มต้นและตำแหน่งสุดท้าย ไม่ได้พิจารณาว่าระหว่างเส้นทางนั้นมีความสูงเปลี่ยนแปลงหรือไม่อย่างไร แต่ในการเลือกขนาดปั๊มนั้น "จำเป็น" ต้องพิจารณาด้วยว่าระหว่างเส้นทางนั้น การเปลี่ยนแปลงความสูง (ในทิศทางที่สูงกว่าตำแหน่งเริ่มต้น) ที่มีค่ามากที่สุดนั้น มีค่าเท่าใด เพราะจำเป็นสำหรับการเริ่มต้นเดินเครื่อง (เดี๋ยวจะยกตัวอย่างให้เห็น)

ตัวอย่างที่ 1 กาลักน้ำ (siphon)

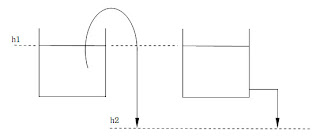
หวังว่าทุกคนคงรู้จักการลักน้ำ ทีนี้ลองพิจารณารูปที่ 1 ข้างล่างซึ่งเป็นการถ่ายน้ำออกจากถังสองใบ โดยระดับน้ำในถังทั้งสองใบอยู่ที่ระดับ h1 เท่ากัน ถังใบซ้ายใช้วิธีเอาปลายข้างหนึ่งของสายยางจุ่มลงไปในถังและปลายอีกข้างหนึ่งปล่อยให้อยู่ต่ำกว่าถังที่ระดับ h2 ส่วนถังใบขวาใช้วิธีเจาะรูด้านข้างถัง และต่อท่อให้ปลายท่ออยู่ต่ำลงมาที่ระดับ h2 เหมือนกัน ถ้าสมมุติให้แรงเสียดทานเนื่องจากการไหลในท่อมีค่าน้อยมากจนตัดทิ้งไปได้ ให้ท่านพิจารณาว่า

(ก) ลองใช้สามัญสำนึกพิจารณาว่า วิธีการแบบไหนจะทำให้มีน้ำไหลออกมาทางปลายท่อที่ระดับ h2

(ข) ถ้าคำนวณโดยใช้สมการของแบร์นูลลี วิธีการแบบไหนจะทำให้มีน้ำไหลออกมาทางปลายท่อที่ระดับ h2

รูปที่ 1 ถังน้ำทั้งสองใบมีระดับน้ำอยู่ที่ h1 เท่ากัน และปลายท่อน้ำไหลออกอยู่ที่ระดับ h2 เท่ากัน

จากการใช้สามัญสำนึก (คงมีกันนะ) คงมองออกว่าการเอาปลายข้างหนึ่งของสายยางจุ่มลงในถังน้ำ และปล่อยให้ปลายอีกข้างหนึ่งอยู่ต่ำกว่าระดับน้ำในถังน้ำนั้น "ไม่สามารถ" ทำให้น้ำไหลออกมาจากถังน้ำตามสายยางได้ (ซึ่งตรงกับความเป็นจริง) แต่ถ้าใช้วิธีการเจาะรูทางด้านข้างถังจะมีน้ำไหลออกมาได้ (ซึ่งก็ตรงกับความเป็นจริงอีก)

แต่ถ้าใช้สมการของแบร์นูลลี (ตามสมการที่ 3) ถ้าขนาดพื้นที่หน้าตัดของถังนั้นใหญ่มากเมื่อเทียบกับพื้นที่หน้าตัดของสายยาง ที่ระดับ h₁ จะพอประมาณได้ว่าความเร็ว v₁ มีค่าเป็น 0 p₁ เท่ากับ p₂ คือความดันบรรยากาศ และทั้งสองวิธีจะมีน้ำไหลออกมาทางปลายท่อที่ระดับ h₂ ได้ ซึ่งไม่ตรงกับความเป็นจริงในกรณีของรูปด้านซ้าย

แล้วการใช้สมการของแบร์นูลลีผิดพลาดตรงไหน

ในการทำกาลักน้ำนั้น เราจะต้อง "เติม" น้ำให้เต็มในสายยางก่อน จากนั้นจึงใช้นิ้วอุดปลายสายยางทั้งสองข้างก่อนที่จะจุ่มปลายข้างหนึ่งลงในถัง และปล่อยให้ปลายอีกข้างหนึ่งอยู่ต่ำกว่าระดับน้ำในถัง เมื่อเราเปิดนิ้วที่อุดรูสายยางอยู่ก็จะทำให้น้ำไหลออกมาจากท่อ ทำให้ความดันในสายยางลดต่ำกว่าความดันบรรยากาศ ความดันบรรยากาศก็จะดันให้น้ำในถังไหลเข้าไปในสายยาง สูงขึ้นไปเหนือระดับปากถัง (ซึ่งอยู่สูงกว่าระดับ h₁) และไหลตกลงมาทางปลายด้าน h₂ ทำให้น้ำไหลได้อย่างต่อเนื่อง (ซึ่งขณะนี้สมการของแบร์นูลลีใช้ได้แล้ว) จะเห็นว่าเส้นทางการไหลของน้ำนั้นมีการไหลไปยังระดับที่สูงกว่าระดับเริ่มต้น (น้ำไหลเองจากที่ต่ำไปยังที่สูงไม่ได้) ซึ่งช่วงนี้การไหลต้องการพลังงานเพื่อที่จะไหลขึ้นไปได้ โดยพลังงานดังกล่าวจะได้กลับคืนมาในช่วงที่ไหลลง

แต่ถ้าเป็นแบบทางรูปด้านขวานั้น น้ำไม่มีเส้นทางการไหลขึ้นไปสูงกว่าระดับที่สูงที่สุดของน้ำ (h₁) ทำให้เมื่อเจาะรูที่ข้างถังน้ำ น้ำก็สามารถไหลออกมาได้ทันที

ตัวอย่างที่ 2 การถ่ายเทของเหลวจากถังทางด้านซ้ายไปยังถังทางด้านขวา

พิจารณาการถ่ายเทของเหลวจากถังทางด้านซ้ายไปยังถังทางด้านขวาที่แสดงในรูปที่ 2 เนื่องจากระหว่างถังทั้งสองมีถนนคั่นกลางอยู่ ดังนั้นวิศวกรจึงวางแผนที่จะเดินท่อแบบ

(ก) ยกสูงข้ามถนน (ตามแนวเส้นสีเขียว) หรือ

(ข) ทำทางลอดใต้ถนน (ตามแนวเส้นสีน้ำเงิน)

คำถามคือทั้งสองวิธีการนั้น (ถ้าค่าการสูญเสียเนื่องจากแรงเสียดทานในท่อนั้นเท่ากัน) จะใช้ปั๊มที่มีขนาดเท่ากันหรือแตกต่างกันอย่างไร

รูปที่ 2 การถ่ายของเหลวโดยใช้ปั๊มสูบของเหลวจากถังทางด้านซ้ายไปยังถังทางด้านขวา h1 คือระดับความสูงของของเหลวในถังด้านซ้าย h2 คือระดับความสูงของของเหลวในถังด้านขวา h3 คือระดับความสูงของถังทั้งสอง (h3 > h2 และ h3 > h1 แต่ h1 และ h2 เปลี่ยนแปลงระดับตลอดเวลาที่ทำการสูบของเหลว) h4 คือระดับความสูงของท่อถ้าหากต้องการยกสูงข้ามถนน (h4 > h3) และ h5 คือระดับความลึกของท่อที่ต้องการเดินลอดถนน ความสูงของตำแหน่งปั๊มให้ถือว่าอยู่ที่ระดับพื้นดิน

ลองเริ่มจากการสมมุติว่าเราไม่มีปั๊ม และระดับน้ำในถังด้านซ้าย (h1) สูงกว่าระดับน้ำในถังด้านขวา (h2) ถ้าเราเอาสมการของแบร์นูลลีมาจับ จะพบว่าสมการของแบร์นูลลีจะบอกว่ามีน้ำไหลจากถังด้านซ้ายไปยังถังด้านขวาได้ไม่ว่าจะเดินท่อยกสูงข้ามถนนหรือลอดใต้พื้นถนน

แต่ถ้าเอาความเป็นจริงมาจับคุณคงจะบอกได้ว่าจะมีน้ำไหลจากถังด้านซ้ายไปยังถังด้านขวาได้เฉพาะในกรณีที่เดินท่อลอดใต้ถนนเท่านั้น ส่วนการเดินท่อยกข้ามถนนไปนั้นจะไม่มีน้ำไหลไปอีกฝั่ง เพราะน้ำไม่สามารถไหลได้เองจากระดับ h1 ขึ้นไปยังระดับท่อที่อยู่เหนือถนน h4 ที่อยู่สูงกว่าได้ แต่ถ้าหากคุณทำให้น้ำไหลขึ้นไปยังระดับ h4 และไหลลงมาอีกทางฝั่งได้ น้ำก็จะไหลต่อเนื่องได้เอง (เหมือนกับกาลักน้ำในตัวอย่างที่ 1)

ในการเลือกขนาดปั๊มนั้น ถ้าคุณใช้สมการของแบร์นูลลีเพียงอย่างเดียว คุณจะได้ปั๊มที่มีเฮดเท่ากับ (ความสูงของถัง + อัตราการไหลที่ต้องการ + แรงเสียดทานในท่อ) ซึ่งค่าเฮดที่ได้นั้นจะไม่มีปัญหาใดถ้าหากคุณเดินท่อ "ลอด" ใต้พื้นถนน แต่ถ้าเป็นการเดินท่อยกสูง "ข้าม" ถนนแล้วล่ะก็ ถ้าค่าเฮดที่คำนวณได้นี้น้อยกว่าค่า h4 ปั๊มของคุณจะไม่มีวันสูบของเหลวข้ามไปยังอีกฟากหนึ่งได้

ดังนั้นในการออกแบบระบบท่อที่สูบของเหลวจากที่หนึ่งไปยังอีกที่หนึ่งนั้น คุณสามารถประมาณได้ว่าขนาดเฮดที่น้อยที่สุดที่ปั๊มจะต้องทำได้คือระยะความสูงที่สูงจากตัวปั๊มมากที่สุด ไม่เช่นนั้นระบบของคุณจะไม่สามารถผลักดันของเหลวให้ไหลไปยังอีกฟากหนึ่งได้

ตัวอย่างที่ 2 นี้แสดงให้เห็นว่าการเลือกขนาดปั๊มนั้นไม่ใช่ดูเฉพาะความสูงที่ตำแหน่งต้นทางกับปลายทาง แต่ต้องพิจารณาความสูงในระหว่างกลางประกอบด้วย

ตัวอย่างที่ 3 แบบไหนน้ำไหลแรงกว่ากัน

พิจารณาการไหลของน้ำออกจากถังออกทางท่อผ่านวาล์วควบคุมอัตราการไหลที่แสดงในรูปที่ 3 ข้างล่าง (โจทย์ข้อนี้ดัดแปลงมาจากปัญหาการติดตั้งวาล์วในการดึงผลิตภัณฑ์ที่เป็นของเหลวออกทางด้านข้างหอกลั่น)

คำถามมีอยู่ว่า ที่ปลายท่อที่ระดับ h4 นั้น น้ำไหลออกมาแรงเท่ากันหรือไม่ (ให้แรงเสียดทานเนื่องจากการไหลในสองระบบนั้นเท่ากัน)

รูปที่ 3 ตำแหน่งการติดตั้งวาล์วควบคุมอัตราการไหล h1 คือระดับผิวบนของน้ำในถัง h2 และ h3 คือระดับตำแหน่งที่ติดตั้งวาล์ว (h2 อยู่สูงกว่า h3) และ h4 คือระดับปลายด้านขาออกของท่อ

ถ้าเอาสมการของแบร์นูลลีมาจับกับระบบทั้งสอง (โดยไม่ได้ดูความเป็นจริงว่าโครงสร้างของระบบเป็นอย่างไร) ก็จะพบว่าความเร็วในการไหลของน้ำในทั้งสองระบบจะขึ้นอยู่กับความแตกต่างของความสูง (h1 - h4) แต่ถ้าใช้สามัญสำนึกพิจารณา คุณก็คงจะรู้สึกว่าระบบทางด้านขวานั้นควรจะให้น้ำไหลแรงกว่าระบบทางด้านซ้าย ซึ่งมันขัดกับสิ่งที่สมการของแบร์นูลลีทำนายไว้ แล้วความผิดพลาดมันอยู่ตรงไหนล่ะ

เวลาที่เราเรียนสมการของแบร์นูลลีนั้น มีข้อสมมุติข้อหนึ่งที่หายไปจากการเรียนคือ มีของเหลวไหลอยู่เต็มพื้นที่หน้าตัดของท่อทั้งสองฝากฝั่งของวาล์ว ในกรณีที่ความต้านทานที่จุดใดจุดหนึ่งของระบบท่อสูงกว่าความต้านทานในส่วน downstream ของตำแหน่งนั้นลงไป จุดนั้นจะเป็นจุดกำหนดอัตราเร็วที่ของไหลนั้นจะเคลื่อนผ่านไปได้

กรณีรูปด้านซ้ายของรูปที่ 3 นั้น ความต้านทานส่วนใหญ่ของระบบจะอยู่ที่ตัววาล์ว ถ้าวาล์วเปิดไม่มาก (หรือเปิดเต็มที่ แต่ตัววาล์ว (เช่น globe valve) เองก็มีความต้านทานสูงกว่าระบบท่อในช่วงถัดไป) อัตราการไหลของน้ำที่ไหลผ่านวาล์วจะขึ้นอยู่กับความแตกต่างของระดับความสูง (h1 - h2) แต่ในกรณีของรูปด้านขวานั้น อัตราการไหลของน้ำที่ไหลผ่านวาล์วจะขึ้นอยู่กับความแตกต่างของระดับความสูง (h1 - h3) ซึ่งมีค่ามากกว่าของกรณีรูปด้านซ้าย

เรื่องตำแหน่งติดตั้งวาล์วและการวางระบบท่อนั้นยังมีเรื่องเล่าจากประสบการณ์ให้ฟังอีกหลายเรื่อง ส่วนใหญ่เป็นเรื่องที่ไม่มีเขียนเอาไว้ในตำรา แต่สามารถนำเอาความรู้ที่เรียนมานั้นมาประยุกต์ใช้อธิบายได้ เอาไว้ค่อย ๆ เล่าให้ฟังเป็นระยะไปก็แล้วกัน

หมายเหตุ : ในโรงงานที่ตั้งกลางแจ้งเช่นพวกโรงกลั่นน้ำมันหรือโรงปิโตรเคมีนั้น ความกว้างของถนนและความสูงของท่อต่าง ๆ ที่ยกข้ามถนนต้องนำเอาขนาดของเครื่องจักรกลต่าง ๆ ที่ต้องใช้ในการก่อสร้างและซ่อมบำรุงเข้ามาพิจารณาด้วย เช่นขนาดรถเครน ซึ่งต้องรู้ความสูงและวงเลี้ยวที่รถต้องใช้เวลาเคลื่อนย้าย สำหรับเส้นทางสัญจรทั่วไปนั้นเรามักจะเห็นป้ายบอกว่า สะพานลอยหรือสายไฟฟ้าต่าง ๆ ที่พาดข้ามถนนมักจะสูงจากพื้นถนนอย่างน้อย 5 เมตร (ระยะความสูงมาตรฐาน)

ในกรณีที่รถบรรทุกนั้นเมื่อบรรทุกอุปกรณ์แล้วมีความสูงเกิน 5 เมตร ถ้าเกินไปมากก็ต้องทำเรื่องวางแผนขออนุญาตยกสะพานลอยออกชั่วคราว (สะพานให้คนข้ามนะ มันยกออกได้ แต่ถ้าเป็นสะพานให้รถข้าม มันยกไม่ได้) และยก (หรือบางครั้งต้องตัดแล้วต่อใหม่) สายไฟที่พาดผ่านออกชั่วคราว

สมัยก่อนที่ยังทำงานอยู่ทางภาคตะวันออก เวลาที่อุปกรณ์ที่มีขนาดใหญ่มากที่ส่งมาจากต่างประเทศต้องระบุให้เรือมาเทียบท่าที่ท่าเรือสัตหีบ (ตอนนั้นยังไม่มีท่าเรือแหลมฉบัง) เพราะถ้าไปที่คลองเตยเมื่อใดจะมีปัญหาไม่สามารถขนย้ายอุปกรณ์ออกจากท่าเรือและเคลื่อนที่ผ่านถนนออกมายังถนนบางนา-ตราดได้ เพราะมันมีสิ่งกีดขวางสารพัดอย่าง แต่ถึงกระนั้นก็เคยมีรายกายปิดถนนสุขุมวิทช่วงจากท่าเรือสัตหีบมายังทางเข้านิคมอุตสาหกรรม (สมัยนั้นเป็นทางลาดยางเล็ก ๆ แค่ 2 ช่องทางจราจร ไหล่ทางยังเป็นหินอยู่เลย ไม่ได้ลาดยางด้วย) เพื่อขนเครื่องปฏิกรณ์ขนาดใหญ่มาตามถนน

ทางฝ่ายผู้ควบคุมการขนส่งไม่เพียงแต่ต้องตรวจสอบเส้นทางว่ามีอะไรขวางอยู่ด้านบน แต่ยังต้องตรวจสอบความแข็งแรงของสะพานที่จะนำรถบรรทุกหนักเคลื่อนที่ผ่านด้วย สำหรับพื้นถนนนั้น การเพิ่มจำนวนล้อจะเป็นการกระจายแรงกดบนพื้นถนน แรงกดของแต่ละล้อบนพื้นถนนก็จะลดลง ป้องกันความเสียหายแก่พื้นถนนได้ ดังนั้นถ้าบรรทุกหนักมากก็เพิ่มจำนวนล้อให้มากขึ้น แต่ในกรณีของสะพานนั้นน้ำหนักทั้งหมดของตัวรถจะถ่ายลงไปที่ระบบคานและเสา (ไม่ได้กระจายไปตามพื้นดินเหมือนวิ่งบนถนน) การเพิ่มจำนวนล้อไม่ได้ช่วยอะไรในการลดน้ำหนักที่สะพานต้องรองรับ