เจาะรูข้างถังที่ตำแหน่งสูงเท่าใด ของเหลวจึงจะพุ่งไปได้ไกลที่สุด MO Memoir : Thursday 8 February 2561

ถัง (Tank) เก็บของเหลวใบหนึ่งมีระดับเก็บของเหลวสูงสุด H₁ ถ้าหากถังนี้มีรูที่ผนังด้านข้าง (เช่นอาจเกิดจากการระเบิดของหน่วยอื่น และมีเศษชิ้นส่วนปลิวมาเจาะทะลุผนังด้านข้าง) ของเหลวที่ฉีดพุ่งออกมาทางรูด้านข้างนั้นจะพุ่งไปได้ไกลสุดเป็นระยะทางเท่าใด
 

บทความเรื่อง "A new approach to the layout of storage tank" ในวารสาร Loss Prevention Bulletin vol. 20 เดือนเมษายน ปีค.ศ. ๑๙๗๘ (พ.ศ. ๒๕๒๑) (ไม่ปรากฏชื่อผู้เขียน) ได้ยกหัวข้อนี้มาเป็นประเด็นในการพิจารณาการออกแบบระยะห่าง (x) ของกำแพงกั้นของเหลว (bund wall หรือ dyke wall) ในการออกแบบ tank farm (ความสูงของกำแพงถูกหนดโดยขนาดพื้นที่ที่กำแพงล้อมรอบและปริมาตรของเหลวใน tank ที่กำแพงนั้นล้อมรอบเอาไว้)

รูปที่ ๑ ระยะทางในแนวราบ x ที่ของเหลวที่พุ่งออกจากรูข้างถังเดินทางไปได้ขึ้นอยู่กับระดับความสูงของตำแหน่งรู ถ้าหากรูดังกล่าวอยู่สูง (เช่นเส้น ก) ความเร็วในการฉีดพุ่งออกมาจะต่ำ เพราะแรงดันของเหลวเหนือระดับรูมีไม่มาก และแม้ว่าระยะเวลาการเดินทางก่อนตกถึงพื้นมีมาก ของเหลวก็จะพุ่งไปได้ไม่ไกล ในทางตรงกันข้ามถ้าหากรูนั้นอยู่ที่ตำแหน่งต่ำเกินไป (เช่นเส้น ค) แม้ว่าความเร็วในการฉีดพุ่งออกมาจะสูง เพราะแรงดันของเหลวเหนือระดับรูมีมาก แต่ระยะเวลาการเดินทางก่อนตกถึงพื้นมีน้อย ของเหลวก็จะพุ่งไปได้ไม่ไกลเช่นกัน

ลองพิจารณาถังในรูปที่ ๑ ที่เก็บของเหลวไว้เต็มถัง โดยระดับความสูงของเหลวในถังคือ H₁ เราจะลองคำนวณดูว่าถ้าหากมีรูข้างถังที่ตำแหน่ง h ต่ำลงมาจากผิวของเหลว ของเหลวนั้นจะฉีดพุ่งไปได้ไกลเท่าใด 
  

ถ้าเราให้ v คือความเร็วของของเหลวที่ฉีดพุ่งออกมาจากถัง จากความรู้ในวิชาฟิสิกส์เบื้องต้นเราจะได้ว่า

ระยะทางการเคลื่อนที่ในแนวราบ x = vt          (1)

ระยะทางการเคลื่อนที่ในแนวดิ่ง y = (1/2)gt²          (2)

เมื่อ g คือค่าความเร่งเนื่องจากแรงดึงดูดของโลก (9.81 m/s²) และ t คือระยะเวลาการเคลื่อนที่ก่อนตกถึงพื้น

จากสมการที่สองเราจะได้ว่าเวลา (t) ที่ของเหลวใช้ในการเคลื่อนที่ก่อนตกถึงพื้นมีค่าเป็น

t = (2y/g)^0.5          (3)

แทนค่าจากสมการที่ (3) กลับเข้าไปในสมการที่ (2) จะได้ว่า

x = v.(2y/g)^0.5          (4)

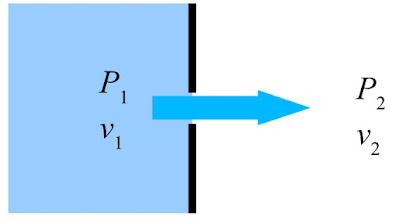
ในกรณีของของเหลวที่ไหลผ่านรูรั่วข้างถัง ถ้าไม่คิดความเสียดทานในการไหลเข้ารูดังกล่าว ความเร็วของของเหลวที่ฉีดพุ่งออกมาจะคำนวณได้จากสมการ

v = (2.ΔP/ρ)^0.5          (5)

เมื่อ ΔP คือผลต่างความดันระหว่างด้านขาเข้าและขาออก ซึ่งในที่นี้คือความดันเนื่องจากระดับความสูงของของเหลวซึ่งเท่ากับ ρgh โดยที่ ρ คือความหนาแน่นของของเหลว ดังนั้นเมื่อแทนค่า ΔP เข้าไปในสมการที่ (5) ก็จะได้ว่า

v = (2gh)^0.5           (6)

(หมายเหตุ : ที่มาของสมการที่ (5) นั้นสามารถอ่านได้ใน Memoir ปีที่ ๙ ฉบับที่ ๑๒๐๙ วันอังคารที่ ๒๖ กรกฎาคม ๒๕๕๙ เรื่อง "เรื่องของ Flow coefficient (Cv)")
 

ค่า v ที่คำนวณได้จากสมการที่ (6) เป็นค่าสูงสุดในทางทฤษฏี เพราะในความเป็นจริงนั้น การไหลเข้า-ออกรูจะมีการสูญเสียพลังงานเนื่องจากความเสียดทานและการไหลปั่นป่วน ขนาดการสูญเสียนี้ขึ้นอยู่กับรูปร่างของรู (เช่นขอบเรียบ ขอบไม่เรียบ) ค่าความสูญเสียนี้แทนด้วยค่า discharge coefficient หรือ C_d ซึ่งเมื่อแทนเข้าไปในสมการที่ (6) ก็จะได้ว่า

v = C_d.(2gh)^0.5           (7)

แทนค่า v ที่ได้จากสมการที่ (7) และค่า y = H₁ - h ลงไปในสมการที่ (4) ก็จะได้ว่า

x = 2C_d.(H₁h - h²)^0.5             (8)

การหาค่า x ที่มากที่สุดทำได้ด้วยการหาค่าอนุพันธุ์ของสมการที่ (8) (dx/dh) และให้มีค่าเท่ากับศูนย์

dx/dh = 0 = C_d.(H₁ - 2h)/(H₁h - h²)^-0.5           (9)
 

หรือ h = H₁/2            (10)

ดังนั้นตำแหน่งรูที่ทำให้ของเหลวฉีดพุ่งไปได้ไกลที่สุดก็คือตำแหน่งตรงกึ่งกลางความสูงนั่นเอง พึงสังเกตว่าตำแหน่งนี้ไม่ขึ้นอยู่กับรูปร่างและขนาดของรู แต่อัตราการรั่วไหลออกขึ้นอยู่กับรูปร่างและขนาดของรู ซึ่งในบทความให้ข้อมูลไว้ว่าในกรณีของรูที่เกิดจากของแข็งปลิวมาเจาะทะลุหรือการกัดกร่อน ผิวรูจะไม่เรียบและการไหลจะเป็นแบบปั่นป่วน C_d ของรูดังกล่าวจะมีค่าประมาณ 0.6
 

แทนค่า h จากสมการที่ (10) และค่า C_d = 0.6 ลงไปในสมการที่ (8) จะได้ระยะทางที่ของเหลวฉีดพุ่งไปได้ไกลสุดคือ

x = 0.6H₁           (11)

ดังนั้น สมมุติว่าเป็นกรณีของถังที่มีความสูง 6 เมตร ตัวกำแพงกั้น (bund wall) ก็ควรอยู่ห่างจากถังอย่างน้อย 3.6 เมตร เพื่อให้มั่นใจว่าถ้าหากมีรูรั่วที่ข้างถัง ของเหลวที่ฉีดพุ่งออกมานั้นจะยังคงอยู่ทางด้านในของกำแพง
 

ค่าที่คำนวณได้นี้เป็นเพียงแค่แนวปฏิบัติหนึ่งเท่านั้นในการป้องกันไม่ให้ของเหลวที่รั่วออกมาจากถังนั้นหลุดออกไปนอกบริเวณกักเก็บ ส่วนที่ว่าในความเป็นจริงนั้นควรมีค่าเป็นเท่าใดก็คงต้องไปดูข้อกำหนดของแต่ละท้องถิ่นว่ากล่าวไว้ว่าอย่างไร เช่นอาจมีการกำหนดระยะห่างที่น้อยที่สุดระหว่างถังกับ bund wall ความสูงที่น้อยและมากที่สุดของ bund wall (เช่นเพิ่มความสูงกำแพง โดยยอมให้ของเหลวพุ่งกระทบผิวกำแพงด้านในแทนที่จะพุ่งข้ามไป) ตัวอย่างเช่นในเอกสาร HSG176 (2nd ed. 2015) Storage of flammable liquids in tanks ในย่อหน้า 161 ได้ให้คำแนะนำว่าสำหรับถังที่มีความจุไม่เกิน 100 m³ ควรมีระยะห่างอย่างน้อย 1 เมตร และถังที่มีความจุตั้งแต่ 100 m³ ขึ้นไปควรมีระยะห่างอย่างน้อย 2 เมตร

รูปที่ ๒ บางส่วนของข้อความจากเอกสาร HSG176 (2nd ed. 2015) Storage of flammable liquids in tanks ที่จัดทำโดย Health and Safety Executive (HSE) ประเทศอังกฤษ

Flow characteristic ของ control valve MO Memoir : Thursday 28 July 2559

วาล์วควบคุมการไหลนั้นมีส่วนประกอบหลัก ๆ อยู่ ๒ ส่วนด้วยกันคือตัววาล์ว (valve body assembly) และส่วนที่ทำหน้าที่ควบคุมระดับการเปิด-ปิดของวาล์ว (actuator) actuator ที่ใช้กันแพร่หลายมากที่สุดเห็นจะได้แก่ชนิดที่ใช้แรงดันลมร่วมกับแรงดันสปริงในการควบคุมระดับการเปิดปิด (ดูรูปที่ ๑ ในหน้าถัดไปประกอบ) ซึ่งอาจจะเป็นการใช้แรงดันลมกดให้วาล์วปิดต้านกับแรงดันสปริงที่พยายามดันให้วาล์วเปิด (เรียกว่าวาล์วชนิด fail-open คือถ้าไม่มีแรงดันลม วาล์วจะอยู่ในตำแหน่งเปิด) หรือใช้แรงดันลมดันให้วาล์วเปิดต้านกับแรงดันสปริงที่ดันให้วาล์วปิด (เรียกว่าชนิด fail-close คือถ้าไม่มีแรงดันลม วาล์วจะอยู่ในตำแหน่งปิด) actuator นี้จะรับสัญญาณควบคุม (ที่อาจเป็นสัญญาณไฟฟ้าหรือนิวเมติกส์) ที่เป็นตัวกำหนดว่าจะให้วาล์วเปิดปิดมากน้อยเท่าใด และจะไปควบคุมระดับความดันอากาศที่ใช้กดแผ่นไดอะแฟรมเพื่อให้วาล์วเปิด-ปิดในระดับที่ต้องการ

 

orifice หรือช่องว่างให้ของเหลวไหลผ่านตัววาล์วมีรูปร่างเป็นวงกลม สำหรับวาล์วแต่ละตัวขนาดพื้นที่ orifice นี้จะคงที่ แต่จะเปิดให้ของไหลไหลผ่านได้มากน้อยเท่าใดนั้นขึ้นอยู่กับรูปร่างของ valve plug และระดับความสูงของ valve plug เมื่อเทียบกับ valve seat (ดูรูปที่ ๒ ประกอบ) ถ้า valve plug ลงมาแนบ valve seat ก็เรียกว่าวาล์วอยู่ในตำแหน่งปิดเต็มที่ (หรือเปิด 0%) ถ้า valve plug ยกตัวขึ้นสูงสุดก็เรียกว่าวาล์วเปิดเต็มที่ (หรือเปิด 100%) และความสัมพันธ์ระหว่างพื้นที่ orifice ที่เปิด (ซึ่งส่งผลต่ออัตราการไหลผ่านตัววาล์วหรือ flow characteristic) ต่อระดับการยกตัวของ valve plug เป็นตัวจำแนกว่าวาล์วตัวดังกล่าวเป็นวาล์วแบบไหน
 

รูปที่ ๑ องค์ประกอบของวาล์วควบคุมแบบที่ใช้กันแพร่หลายมากที่สุด (จากหน้า 7 ของหนังสือ Control valve handbook, 3rd ed. ของบริษัท Fisher control international, INC.) ในรูปตัววาล์วเป็นชนิด globe valve ใช้แรงดันลม (ทำงานผ่าน actuator) ในการควบคุมระดับการเปิด-ปิดของวาล์ว

รูปที่ ๒ Orifice pass area เป็นพื้นที่ที่ให้ของไหลไหลผ่านได้ ขนาดของพื้นที่นี้ขึ้นอยู่กับรูปร่างของ valve plug และระดับการยกตัวของ valve plug เมื่อเทียบกับ valve seat ในตัวอย่างในรูปนี้ที่ตำแหน่งวาล์วปิดเต็มที่ถือว่าระดับการเปิดเป็น 0% ที่ตำแหน่งวาล์วเปิดเต็มที่ถือว่าระดับการเปิดเป็น 100%

(รูปจาก http://www.spiraxsarco.com/Resources/Pages/Steam-Engineering-Tutorials/control-hardware-el-pn-actuation/control-valve-characteristics.aspx)

รูปที่ ๓ แสดงกราฟความสัมพันธ์ระหว่างอัตราการไหลและระดับการยกตัวของ valve plug ของกรณีสมมุติกรณีหนึ่งโดยสมมุติให้อัตราการไหลผ่านวาล์วเมื่อวาล์วเปิดเต็มที่คือ 10 m³/hr และค่าความดันลดคร่อมตัววาล์วคงที่ (คือไม่ขึ้นกับระดับการเปิดของวาล์ว)
 

วาล์วชนิด fast opening หรือ quick opening นั้นอัตราการไหลจะเพิ่มขึ้นอย่างรวดเร็วในช่วงแรกเมื่อ valve plug เริ่มยกตัวจนเข้าหาค่าสูงสุด จากนั้นจะไม่ค่อยเปลี่ยนแปลงตามระยะการยกตัวของ valve plug เท่าใดนัก วาล์วชนิดนี้มักจะใช้กับงานควบคุมที่ต้องการเพียงแค่การปิด สนิทหรือเปิดเต็มที่เท่านั้น (งานประเภท on-off)
 

วาล์วชนิดที่สองมีรูปแบบความสัมพันธ์ระหว่างอัตราการไหลและระดับการยกตัวของ valve plug ที่เป็นเส้นตรง (linear characteristic) กล่าวคืออัตราการไหลผ่านจะแปรผันตรงกับระดับการยกตัวของ valve plug กล่าวคือถ้า valve plug ยกตัวสูงขึ้น 20% ของระยะการยกตัวสูงสุด อัตราการไหลผ่านก็จะมีค่าเท่ากับ 20% ของอัตราการไหลผ่านสูงสุด ถ้า valve plug ยกตัวสูงขึ้น 65% ของระยะการยกตัวสูงสุด อัตราการไหลผ่านก็จะมีค่าเท่ากับ 65% ของอัตราการไหลผ่านสูงสุดเช่นกัน
 

วาล์วชนิดที่สามเรียกว่าชนิด equal percentage โดยในทางทฤษฎีนั้น อัตราการไหลผ่านวาล์วที่ระยะการยกตัวของ valve plug ต่าง ๆ นั้นเป็นไปตามสมการ

รูปที่ ๓ ตัวอย่างกราฟแสดงความสัมพันธ์ระหว่างอัตราการไหลและ %Valve lift ของวาล์วชนิด Quick openin, Linear และ Equal percentage ที่มีค่า rangeabiligy ต่างกัน (ค่าตัวเลขแสดงไว้ในตารางที่ ๑)

ค่า rangeability คือค่าอัตราส่วนระหว่างอัตราการไหลสูงสุดต่ออัตราการไหลต่ำสุดที่วาล์วตัวนั้นสามารถควบคุมได้ สำหรับ globe valve นั้นจากข้อมูลที่ค้นในอินเทอร์เน็ตบางแหล่งให้ค่ากลาง ๆ ไว้ที่ 50 ในขณะที่บางเว็บบอร์ดนั้นแนะนำไว้ที่ประมาณ 20 และในแคตตาล็อกของผู้ผลิตวาล์วบางรายนั้นให้ค่าสูงถึงระดับหลายร้อย วาล์วที่มีค่า rangeability สูงแสดงว่าสามารถควบคุมการไหลเมื่อวาล์วเปิดไม่มาก (หรือที่อัตราการไหลต่ำ) ได้ดี แต่ก็มีการแนะนำเหมือนกันว่าในการเลือกขนาดวาล์วควบคุมนั้นไม่ควรที่เลือกขนาดวาล์วที่ทำให้วาล์วต้องทำงานในตำแหน่งที่เกือบปิดสนิทหรือเปิดเกือบเต็มที่
  

เพื่อให้เห็นภาพความสัมพันธ์ระหว่างอัตราการไหลผ่านวาล์วและระยะการยกตัวของวาล์วชนิด equal percentage จะลองคำนวณโดยใช้สมการที่ (1) โดยกำหนดให้วาล์วมีค่า Q_max = 10 m³/hr และมีค่า rangeability (τ) = 20 50 และ 100 ผลการคำนวณที่ได้แสดงไว้ในตารางที่ ๑ ข้างล่าง
 

ในทางปฏิบัตินั้นค่าอัตราการไหลที่ %Valve lift = 0% จะต้องมีค่าเป็นศูนย์ไม่ว่าวาล์วตัวนั้นจะมีค่า rangeability เท่าใด ตัวเลขที่ไม่ใช่ศูนย์ในตารางเป็นตัวเลขที่ได้มาจากสมการที่ (1) 
  

ตัวเลข %Increase แสดง %อัตราการไหลที่เพิ่มขึ้นเมื่อเทียบกับอัตราการไหลก่อนหน้า ตัวอย่างเช่นในกรณีของวาล์วที่มีค่า τ = 20 เมื่อ %Valve lift = 20% จะมีอัตราการไหลเท่ากับ 0.91 m³/hr และเมื่อ %Valve lift เพิ่มขึ้นอีก 10% เป็น 30% จะมีอัตราการไหลเท่ากับ 1.23 m³/hr ดังนั้นอัตราการไหลที่เพิ่มขึ้นเมื่อคิดเป็น % แล้วจะเท่ากับ (1.23 - 0.91)/0.91 x 100 = 34.9% และในทำนองเดียวกันที่ %Valve lift = 60% จะมีอัตราการไหลเท่ากับ 3.02 m³/hr และเมื่อ %Valve lift เพิ่มขึ้นอีก 10% เป็น 70% จะมีอัตราการไหลเท่ากับ 4.07 m³/hr ดังนั้นอัตราการไหลที่เพิ่มขึ้นเมื่อคิดเป็น % แล้วจะเท่ากับ (4.07 - 3.02)/3.02 x 100 ซึ่งก็เท่ากับ 34.9% เช่นกัน
 

ในทำนองเดียวกันจะเห็นว่าในกรณีของวาล์วที่มีค่า τ = 50 นั้นเมื่อวาล์วเปิดเพิ่มขึ้น 10% จากค่าเดิม อัตราการไหลจะเพิ่มขึ้น 47.9% (ไม่ขึ้นอยู่กับว่า %Valve lift เดิมนั้นมีค่าเท่าใด) และในกรณีของวาล์วที่มีค่า τ = 100 นั้นเมื่อวาล์วเปิดเพิ่มขึ้น 10% จากค่าเดิม อัตราการไหลจะเพิ่มขึ้น 58.5% (โดยไม่ขึ้นอยู่กับว่า %Valve lift เดิมนั้นมีค่าเท่าใดเช่นกัน)
 

ตัวอย่างการคำนวณในที่นี้ผมอิงจากหน้าเว็บของบริษัท Spirax sarco ที่ไปดึงเอารูปที่ ๒ มา โดยนำมาขยายความเพื่อให้ผู้ที่ไม่ค่อยมีความรู้พื้นฐานหรือว่ากำลังศึกษาอยู่นั้น (หรือพื้นภาษาอังกฤษไม่ดี) สามารถมองเห็นภาพได้ชัดเจนขึ้น

ปิดท้ายด้วยรูป control valve และระบบ piping ของโรงงานแห่งหนึ่งที่ถ่ายไว้เมื่อ ๒ ปีที่ในขณะที่ไปเดินตรวจสอบหลังการติดตั้ง ดูออกไหมครับว่าการติดตั้งมันมีอะไรไม่ถูกต้องอยู่ ขออนุญาตไม่เฉลยนะครับ :) :) :)

เรื่องของ Flow coefficient (Cv) MO Memoir : Tuesday 26 July 2559

เวลาที่ใครสักคนต้องทำงานออกแบบเพื่อหาขนาดของวาล์วควบคุมเพื่อให้ได้อัตราการไหลตามต้องการนั้น มักจะเจอพารามิเตอร์หนึ่งที่เกี่ยวข้องกับตัววาล์วปรากฏเข้ามาที่มีชื่อว่า "Flow coefficient" หรือที่เรียกย่อ ๆ ว่า C_v ที่แสดงความสัมพันธ์ระหว่างอัตราการไหล (Q) และค่าความดันลด (ΔP) คร่อมวาล์วตัวนั้นตามสมการ

เมื่อ Q คืออัตราการไหลในหน่วย gallon per min (ส่วนจะเป็นแกลลอนอเมริกาหรือแกลลอนอังกฤษก็ค่อยว่ากันอีกที) ΔP คือค่าความดันลดคร่อมวาล์ว (pressure drop) ในหน่วย psi SG คือค่าความถ่วงจำเพาะ (specific gravity) ของของเหลว
 

ในการหาค่า C_v นั้น ถ้าเป็นแบบอเมริกาจะทำการทดลองด้วยการอัตราการไหลของน้ำ (US gal per min) ที่อุณหภูมิ 60ºF ที่ความดันลดคร่อมตัววาล์ว 1 psi โดยให้น้ำมีค่าความถ่วงจำเพาะเท่ากับ 1 ดังนั้นเมื่อแทนค่าต่าง ๆ เข้าไปในสมการที่ (1) ก็จะเห็นว่าค่า C_v ก็คือค่าอัตราการไหลของน้ำที่อุณหภูมิ 60ºF ที่ไหลผ่านวาล์วโดยมีค่าความดันลดคร่อมตัววาล์วเท่ากับ 1 psi (ต่อไปในที่นี้ถ้าหากมีการกล่าวถึงหน่วย "แกลลอน" จะหมายถึง US gal ซึ่งเท่ากับ 3.785 ลิตร เว้นแต่จะมีการระบุว่าเป็น Imperial gallon หรือแกลลอนอังกฤษซึ่งเท่ากับ 4.546 ลิตร)
 

ดังนั้นถ้าว่ากันตามนี้ สมมุติว่าเรามีวาล์วตัวหนึ่งที่มีค่า C_v = 20 ที่ใช้ในการควบคุมการไหลของน้ำ
 

ถ้าแรงดันน้ำด้านขาเข้าวาล์วคือ 30 psi แรงด้านน้ำด้านขาออกคือ 29 psi (ΔP = 1) อัตราการไหลของน้ำผ่านวาล์วตัวนี้ที่คำนวณได้จากสมการที่ (1) คือ 20 gal/min
 

ถ้าแรงดันน้ำด้านขาเข้าวาล์วคือ 30 psi แรงด้านน้ำด้านขาออกคือ 27 psi (ΔP = 3) อัตราการไหลของน้ำผ่านวาล์วตัวนี้ที่คำนวณได้จากสมการที่ (1) คือ 34.6 gal/min
 

ถ้าแรงดันน้ำด้านขาเข้าวาล์วคือ 60 psi แรงด้านน้ำด้านขาออกคือ 59 psi (ΔP = 1) อัตราการไหลของน้ำผ่านวาล์วตัวนี้ที่คำนวณได้จากสมการที่ (1) คือ 20 gal/min
 

หรือจะมองว่าค่า C_v คือค่าที่บอกความสามารถของวาล์วว่ายอมให้น้ำไหลผ่านได้ในอัตราเท่าใดที่ค่า ΔP ต่าง ๆ ก็ได้

แต่มีคำถามหนึ่งที่เชื่อว่ามีใครหลายต่อหลายคนสงสัยก็คือ "สมการที่ (1) นั้นมันมาได้อย่างไร"

จากการที่ได้พิจารณา (และค้นคว้าเอาเอง) ก็พบว่าสมการนี้น่ามาจาก Bernoulli's equation ที่มีการใส่ข้อสมมุติต่าง ๆ เข้าไปเพื่อให้รูปแบบสมการง่ายขึ้น
 

เพื่อให้เห็นภาพ ขอให้พิจารณากรณีของการไหลของของเหลวที่อัดตัวไม่ได้ผ่าน orifice (คือรูกลม ๆ) ดังตัวอย่างที่แสดงในรูปที่ ๑ (P คือความดัน v คือความเร็วของการไหล ρ คือความหนาแน่นของของเหลว ตัวห้อย 1 คือด้านขาเข้า ตัวห้อย 2 คือด้านขาออก)

รูปที่ ๑ การไหลของน้ำผ่าน orifice

Bernoulli's equation ที่ใช้อธิบายการไหลของน้ำผ่าน orifice ดังกล่าวมีหน้าตาดังนี้

เนื่องจากด้านขาเข้าและด้านขาออกนั้นอยู่ที่ระดับความสูงเดียวกัน (h₁ = h₂) และสมมุติให้ไม่มีการสูญเสียพลังงานเนื่องจากความเสียดทาน (loss = 0) ดังนั้นเมื่อจัดรูปแบบสมการที่ (2) ใหม่เราจะได้ว่า

ถ้าสมมุติต่อว่า v₁ << v₂ ดังนั้นค่า v₂² - v₁² จะประมาณได้เท่ากับ v₂² เราจะสามารถเขียนสมการที่ (3) ได้ในรูปแบบ

ถ้าให้ Q คืออัตราการไหลโดยปริมาตร และ A คือพื้นที่หน้าตัดของ orifice จากความสัมพันธ์ v₂ = Q/A เมื่อแทนความสัมพันธ์ดังกล่าวลงในสมการที่ (4) จะได้ว่า

ถึงจุดนี้พอจะมองเห็นความคล้ายคลึงกันระหว่างสมการที่ (1) กับสมการที่ (6) ไหมครับ
 

จากสมการที่ (5) จะเห็นว่าค่าพารามิเตอร์ที่บ่งบอกคุณสมบัติของ orifice ที่ปรากฏอยู่ในสมการนั้นมีเพียงค่าพื้นที่หน้าตัดการไหล A เท่านั้น แต่ในความเป็นจริงนั้นมันยังมีปัจจัยอื่นเข้ามาเกี่ยวข้องอีก เช่นรูปร่างพื้นที่หน้าตัด ลักษณะของขอบ orifice (เช่น ขอบเรียบตัด ขอบโค้งมน ขอบปาดเข้า ขอบบานออก ฯลฯ) ฯลฯ ดังนั้นจะเป็นการง่ายขึ้นถ้าเรารวมผลของปัจจัยต่าง ๆ เหล่านี้ไว้ในค่า C (คือ C ไม่ได้ขึ้นอยู่กับพื้นที่เพียงอย่างเดียว) แล้วไปหาค่า C จากการทดลองเอา
 

เส้นทางการไหลผ่านวาล์วนั้นไม่เรียบง่ายเหมือนการไหลผ่าน orifice เพราะมีทั้งการไหลเส้นทางการไหลที่เลี้ยวโค้งไปมาและไหลผ่านรูที่ใช้ในการควบคุมการไหล ค่า C_v หรือ Flow efficient จึงเปรียบเสมือนค่าที่รวบรวมพารามิเตอร์ต่าง ๆ ที่ส่งผลต่อการไหลผ่านตัววาล์ว (ไม่ว่าจะเป็นขนาดของช่องเปิด จำนวนของช่องเปิด ความคดเคี้ยวของเส้นทางการไหล ฯลฯ) เอาไว้ในพารามิเตอร์ตัวเดียวคือ C_v ค่า C_v นี้เปรียบเสมือนพารามิเตอร์ตัวที่ใช้บอกว่าวาล์วแต่ละตัวนั้นให้ของไหลไหลผ่านได้เหมือนกันหรือไม่ (โดยไม่ต้องสนใจว่าโครงสร้างข้างในจะเป็นอย่างไร) ซึ่งหาได้จากการทดลอง ดังนั้นในการเปรียบเทียบความสามารถของวาล์วในการยอมให้ของไหลไหลผ่านนั้นจึงต้องกระทำที่สภาวะการทดสอบเดียวกัน
 

ในระบบอเมริกานั้นจะทำการทดลองด้วยการวัดอัตราการไหลของน้ำ (ในหน่วย US gal per min) ที่อุณหภูมิ 60ºF ที่ไหลผ่านวาล์วโดยมีความดันลดคร่อมตัววาล์ว 1 psi โดยให้น้ำมีค่าความถ่วงจำเพาะเท่ากับ 1 ในกรณีนี้ค่า C_v จะมีหน่วยเป็น US gal/min ถ้าจะเปลี่ยนค่านี้เป็น Imperial gal ก็ต้องคูณด้วย 0.8326 (มาจาก 3.785/4.546)
 

ในกรณีของระบบเมตริกนั้นเพื่อป้องกันการสับสน จึงมีการหันไปใช้สัญลักษณ์ K_v (บางทีก็เรียกว่า Flow factor) แทน C_v โดย

รูปที่ ๒ ค่า C_v สำหรับของไหลที่ไม่ใช่น้ำ (จากหน้า 99 ของเอกสาร Valve and valve actuator selection guide ของบริษัท SIEMENS ดาวน์โหลดไฟล์ pdf ได้ที่

http://w3.siemens.com.br/buildingtechnologies/br/pt/automacao-predial/dc/Documents/Valvulas.pdf)

ในกรณีของระบบเมตริกนี้อัตราการไหลจะมีหน่วยเป็น m³/hr ในขณะที่ความดันมีหน่วยเป็น bar (หรือ kg/cm²) โดยนิยามของ K_v คืออัตราการไหลของของเหลวตัวกลางที่ไหลผ่านวาล์ว (m³/hr) เมื่อมีความดันลดคร่อมวาล์ว 1 kg/cm² และวาล์วเปิดเต็มที่ โดยให้ของเหลวที่ไหลผ่านวาล์วมีค่า specific gravity เท่ากับ 1.0 และค่า kinematic viscosity 10^-6 m²/s (ซึ่งก็คือน้ำนั่นเอง)

ที่เล่ามาข้างต้นก็เพื่อเป็นพื้นฐานให้ทำความรู้จักกับค่า C_v โดยยกตัวอย่างกรณีของไหลที่ง่ายที่สุดคือน้ำ ในกรณีของของเหลวที่มีคุณสมบัติที่แตกต่างไปจากน้ำมาก (เช่นมีความหนืดที่แตกต่างมา) หรือเป็นแก๊ส (คือเป็นของไหลที่อัดตัวได้) นิยามการคำนวณค่า C_v จะแตกต่างออกไป รูปที่ ๒ ข้างต้นเป็นตัวอย่างการคำนวณค่า C_v สำหรับของไหลชนิดอื่นที่ไม่ใช่น้ำ

อ่านเรื่องเกี่ยวกับ Flow coefficient เพิ่มเติมได้ที่

http://www.spiraxsarco.com/Resources/Pages/Steam-Engineering-Tutorials/control-hardware-el-pn-actuation/control-valve-capacity.aspx

https://en.wikipedia.org/wiki/Flow_coefficient

ด้วยเหตุที่ว่าหน้ากระดาษยังเหลือ ก็เลยขอปิดท้ายด้วยรูปของอาคารอะไรก็ไม่รู้ที่สร้างอยู่บนชั้นดาดฟ้าของอาคารข้างเคียงแลปเรา เห็นข้างในเต็มไปด้วยขวดน้ำพลาสติกและกระถางต้นหญ้า ไม่รู้เหมือนกันว่าเป็นงานของวิศวกรรมโยธาหรือสิ่งแวดล้อม