การคำนวณเชิงตัวเลข (๓๕) การแก้สมการอนุพันธ์ด้วยฟังก์ชันพหุนาม (๑๐) MO Memoir : Thursday 16 April 2563

ฉบับนี้เป็นฉบับต่อจากตอนที่แล้ว (ฉบับวันเสาร์ที่ ๑๑ เมษายน ๒๕๖๓ ที่ผ่านมา) แต่คราวนี้จะเป็นกรณีของพิกัดทรงกระบอก (cylindrical) และทรงกลม (spherical)

เริ่มจากกรณีของตัวเร่งปฏิกิริยารูปทรงกระบอกที่มีรัศมี r = 1 หน่วย และมีความยาวเป็นอนันต์ (เพื่อตัดผลที่หัวท้ายออกไป ให้มีเฉพาะการแพร่ในทิศทางแนวรัศมีเท่านั้น) ในกรณีนี้สมการดุลมวลสารอย่างง่ายจะมีหน้าตาดังนี้ ....

ดาวน์โหลดบทความ pdf ฉบับเต็มได้ที่ลิงก์นี้

การคำนวณเชิงตัวเลข (๓๐) การแก้สมการอนุพันธ์ด้วยฟังก์ชันพหุนาม (๕) MO Memoir : Wednesday 18 March 2563

หลังจากทิ้งเรื่องนี้ไป ๕ ปีเศษ (จากธันวาคม ๒๕๕๗) ก็ได้เวลากลับมาเขียนเรื่องนี้ต่อ คือ Memoir ฉบับนี้เป็นตอนต่อจากฉบับก่อนหน้านี้ดังนี้

ปีที่ ๒ ฉบับที่ ๑๗๔ วันอาทิตย์ที่ ๒๐ มิถุนายน ๒๕๕๓ เรื่อง "การคำนวณเชิงตัวเลข (๑) การแก้สมการอนุพันธ์ด้วยฟังก์ชันพหุนาม"

ปีที่ ๒ ฉบับที่ ๑๗๕ วันจันทร์ที่ ๒๑ มิถุนายน ๒๕๕๓ เรื่อง "การคำนวณเชิงตัวเลข (๒) การแก้สมการอนุพันธ์ด้วยฟังก์ชันพหุนาม"

ปีที่ ๗ ฉบับที่ ๘๙๖ วันพฤหัสบดีที่ ๒๗ พฤศจิกายน ๒๕๕๗ เรื่อง "การคำนวณเชิงตัวเลข (๕) การแก้สมการอนุพันธ์ด้วยฟังก์ชันพหุนาม"

ปีที่ ๗ ฉบับที่ ๘๙๙ วันพุธที่ ๓ ธันวาคม ๒๕๕๗ เรื่อง "การคำนวณเชิงตัวเลข (๖) การแก้สมการอนุพันธ์ด้วยฟังก์ชันพหุนาม"

ทั้ง ๔ เรื่องข้างต้นถูกนำไปรวมไว้ใน "MO Memoir รวมบทความชุดที่ ๑๖ วิศวกรรมเคมีภาคคำนวณ" ที่สามารถดาวน์โหลดไฟล์ pdf ได้จากหน้า blog

ในตอนที่ ๑ (ฉบับที่ ๑๗๔) และตอนที่ ๒ (ฉบับที่ ๑๗๕) ของเรื่องนี้ ได้แสดงให้เห็นว่าการเลือกจุดที่กำหนดให้ค่า residual เป็นศูนย์นั้น (จุดที่เรียกว่า collocation point) ส่งผลต่อความถูกต้องของคำตอบที่ได้ แต่โดยหลักก็คือตำแหน่งของจุดที่เลือกนั้นควรเป็นบริเวณที่คำตอบมีการเปลี่ยนแปลงรวดเร็วเมื่อเทียบกับบริเวณอื่น แต่เนื่องจากในหลายกรณีเรามักไม่รู้ว่าคำตอบที่ได้นั้นจะมีการเปลี่ยนแปลงอย่างใด จึงได้มีการนำเสนอว่าถ้าเราประมาณคำตอบด้วย orthogonal polynomial จุดที่เลือกก็ควรเป็น root (จุดที่ค่าฟังก์ชันเป็นศูนย์) ของ orthogonal polynomial และในตอนที่ ๔ ของเรื่องนี้ (ฉบับที่ ๘๙๙) ก็ได้ทิ้งท้ายว่าจะหาเวลามาเขียนเรื่องนี้ต่อ แต่ไม่รู้เหมือนกันว่าทำไมถึงลืมเรื่องนี้ไปได้ วันนี้ก็เลยขอมาเขียนต่อ โดยขอเป็นเรื่อง "Orthogonal function" หรือที่มีคนแปลเป็นไทยว่า "ฟังก์ชันเชิงตั้งฉากก็แล้วกัน" ก็แล้วกัน

บทความฉบับเต็มในรูปแบบไฟล์ pdf อ่านได้ที่ลิงก์นี้

การคำนวณเชิงตัวเลข (๒๓) การแก้ปัญหาสมการเชิงอนุพันธ์สามัญปัญหาเงื่อนไขค่าเริ่มต้นด้วยระเบียบวิธี Bogacki-Shampine และ Predictor-Evaluator-Corrector-Evaluator (PECE) MO Memoir : Monday 27 August 2561

ผมมักจะตั้งคำถามนิสิตที่ทำวิจัยโดยมีการสร้างแบบจำลองทางคณิตศาสตร์เสมอว่า วัตถุประสงค์ของการสร้างแบบจำลองนั้นคืออะไร เพราะมันใช้เกณฑ์ในการพิจารณาความเหมาะสมที่แตกต่างกัน ในกรณีของแบบจำลองที่นำไปใช้เพื่อการออกแบบหรือจำลองกระบวนการจริงเพื่อการศึกษานั้น จะให้ความสำคัญไปที่ความถูกต้องของคำตอบที่ได้ แต่ถ้าวัตถุประสงค์เป็นเพื่อการควบคุมกระบวนการในเวลาจริง จะให้ความสำคัญไปที่ความเร็วในการคำนวณ กล่าวคืออย่างน้อยจะต้องได้คำตอบโดยประมาณว่ากำลังจะเกิดอะไรขึ้น โดยต้องมีเวลาเหลือพอสำหรับให้ระบบควบคุมทำการปรับแก้
 

ในการแก้ปัญหาระบบสมการอนุพันธ์สามัญ ปัญหาเงื่อนไขค่าเริ่มต้นนั้น คงปฏิเสธไม่ได้ว่าระเบียบวิธีหลักที่ใช้กันส่วนใหญ่ในการแก้ปัญหาคือระเบียบวิธีในกลุ่มรุงเก-คุตตาอันดับ ๔ (4th order Runge-Kutta) ที่พัฒนาโดยใช้ระเบียบวิธีนี้เป็นพื้นฐาน ด้วยเหตุผลหลายประการได้แก่ การที่มันเป็นระเบียบวิธีที่สามารถเริ่มต้นการคำนวณด้วยตนเองได้ (เป็น single step method) เป็นระเบียบวิธีโดยแจ้ง (เป็น explicit method) ทำให้ไม่มีปัญหากับสมการที่ไม่เป็นเชิงเส้น (non-linear) ให้ความถูกต้องของคำตอบสูง และมีค่า step size ของการอินทิเกรตที่ค่อนข้างกว้าง แต่ในกรณีที่ต้องการความรวดเร็วสูงในการคำนวณโดยความถูกต้องของคำตอบเป็นรอง ระเบียบวิธีในกลุ่มนี้ก็ไม่ใช่ตัวเลือกที่ดีนัก หรือในกรณีของสมการที่มีปัญหาเรื่อง stiffness หรือไวสูงต่อการสะสมค่าความคลาดเคลื่อนในการคำนวณ ก็อาจจะใช้การไม่ได้เลย
 

ด้วยเหตุนี้แม้แต่ในโปรแกรมสำเร็จรูปเช่น MATLAB ที่นิยมใช้กันอยู่ในขณะนี้ ก็ยังมีระเบียบวิธีสำหรับการแก้ปัญหาระบบสมการอนุพันธ์สามัญ ปัญหาเงื่อนไขค่าเริ่มต้น ให้เลือกเกือบสิบระเบียบวิธี โดย ODE45 ที่ใช้ระเบียบวิธีที่พัฒนาโดยอิงจากรุงเก-คุตตาอันดับ ๔ เป็นฐาน ก็เป็นเพียงแค่ตัวเลือกหนึ่งเท่านั้นเอง
 

วันนี้จะลองกลับมาพิจารณาตัวอย่างที่เคยยกมาใน Memoir ฉบับวันพุธที่ ๑๕ สิงหาคมและวันอาทิตย์ที่ ๑๙ สิงหาคมที่ผ่านมา โดยจะทดลองใช้ระเบียบวิธีอื่นในการแก้ปัญหาดูบ้าง
 

ดาวน์โหลดไฟล์ pdf ฉบับเต็มได้ที่ลิงค์นี้ 

รู้ทันนักวิจัย (๑๖) เริ่มต้นดีใช่ว่าจะเดินต่อไปได้ดี MO Memoir : Sunday 19 August 2561

" ... ตัวอย่างที่ยกมานี้เป็นกรณีของปัญหาที่เรียกว่า "Stiff equation" กล่าวคือตัวแปรหนึ่งมีการเปลี่ยนแปลงอย่างรวดเร็วจนไปเข้าที่ที่ค่า ๆ หนึ่งในช่วงสั้น ๆ ในขณะที่ตัวแปรอีกตัวหนึ่งนั้นมีการเปลี่ยนแปลงที่ช้ากว่า ในกรณีเช่นนี้การเปลี่ยนแปลงอย่างรวดเร็วของตัวแปรตัวแรกเป็นตัวกำหนด step size ของการคำนวณว่าต้องใช้ความยาวช่วงก้าวที่สั้นมากในช่วงแรก แต่แม้ว่าพอพ้นช่วงที่ตัวแปรตัวแรกนั้นแทบจะไม่มีการเปลี่ยนแปลงแล้ว (อย่างเช่นในตัวอย่างที่ยกมานี้จะเห็นว่า A มีค่าใกล้ศูนย์มากแล้ว) การเปลี่ยนแปลงในช่วงหลังจะเป็นของอีกตัวแปรหนึ่งเป็นหลัก (ในที่นี้คือ B) ที่มีการเปลี่ยนแปลงอย่างช้า ๆ แต่กลับพบว่าถ้าเลือกระเบียบวิธีคำนวณที่ไม่เหมาะสม จะไม่สามารถเพิ่มความยาวช่วงก้าวให้กว้างมากขึ้นได้ เพราะจะทำให้การคำนวณนั้นไม่มีเสถียรภาพ ดังเช่นที่เกิดกับระเบียบวิธีรุงเก-คุตตาอันดับ 4 ในที่นี้ (คือการแกว่งของคำตอบที่คำนวณได้) แต่ไม่เกิดกับระเบียบวิธีออยเลอร์โดยนัย
  ....

ปัญหาเช่นนี้เคยเห็นกับผู้ที่ทำวิจัยด้าน simulation ที่ใช้แบบจำลองทางคณิตศาสตร์ที่ผู้อื่นสร้างเอาไว้ (เช่นเครื่องปฏิกรณ์เคมีหรือหอกลั่น) มาใช้เป็นแบบจำลองในงานของตัวเอง ก่อนที่จะทำการปรับเปลี่ยนพารามิเตอร์ของแบบจำลองนั้นหรือผลกระทบจากภายนอกที่จะมีต่อแบบจำลองนั้น โดยการทำงานนั้นผู้วิจัยมักจะนำเอาสมการจากบทความอ้างอิงมาเขียนเป็นโปรแกรมคอมพิวเตอร์แล้วทดสอบโปรแกรมดังกล่าวด้วยการใส่พารามิเตอร์เดียวกันกับที่ใช้ในบทความอ้างอิง แล้วดูว่าคำตอบที่ได้นั้นเหมือนกับของบทความอ้างอิงนั้นหรือไม่ ถ้าพบว่าคำตอบที่ได้นั้นออกมาเหมือนกัน ก็จะถือว่าสมการแบบจำลองที่ตัวเองจะใช้งานต่อไปนั้นได้รับการยืนยันความถูกต้อง (verification) แล้ว
 ...

ปัญหามันเกิดขึ้นจากการที่ในช่วงค่าพารามิเตอร์ที่บทความที่อ้างอิงมานั้นใช้ ระเบียบวิธีที่บทความที่อ้างอิงมานั้นเลือกมาใช้ มันเหมาะสมกับพารามิเตอร์ในช่วงดังกล่าว แต่พอมีการปรับเปลี่ยนพารามิเตอร์ (คือไม่ได้ไปยุ่งอะไรกับตัวโปรแกรม ทำเพียงแค่เปลี่ยนค่าตัวเลขที่ป้อนเข้าไปเท่านั้น) การคำนวณจะเกิดปัญหา ถ้าผู้วิจัยไม่รู้ว่าปัญหาเกิดจากระเบียบวิธิที่เลือกใช้นั้นใช้ไม่ได้กับพารามิเตอร์ในช่วงที่เขาทดลอง ก็มีสิทธิที่จะแปลผลคำตอบที่ได้ว่าเป็นการค้นพบใหม่
 ...

บางครั้งสิ่งที่พบเจอจากการคำนวณก็ไม่ใช่การค้นพบใหม่ แต่เป็นผลจากความไม่รู้ว่าเครื่องมือแต่ละชนิดมีข้อจำกัดอย่างไร และสถานการณ์ไหนควรเลือกใช้เครื่องมือตัวไหน ถ้ามันมีเครื่องมือตัวเดียวที่สามารถใช้งานได้ทุกสถานการณ์ ตัวโปรแกรมก็คงไม่ต้องมีตัวเลือกให้เลือกว่าจะเลือกใช้เครื่องมือตัวไหน ค่า default เป็นเพียงแค่ค่าเริ่มต้นที่ยังสามารถปรับเปลี่ยนได้ ไม่ใช่พารามิเตอร์ที่ห้ามแตะต้อง ..."

ดาวน์โหลดบทความ pdf ฉบับเต็มได้ที่ลิงค์นี้

การแก้สมการเชิงอนุพันธ์สามัญด้วยการใช้ Integrating factor MO Memoir : Wednesday 15 August 2561

"... ตัวอย่างของปฏิกิริยาประเภทนี้ในงานทางวิศวกรรมเคมีได้แก่ปฏิกิริยา partial oxidation และ thermal cracking ไฮโดรคาร์บอน ในปฏิกิริยา partial oxidation นั้น ไฮโดรคาร์บอนหรือสารอินทรีย์ตัวอื่นที่เป็นสารตั้งต้น (A) จะถูกออกซิไดซ์ด้วยออกซิเจนจากอากาศที่ป้อนเข้าไป โดยมีตัวเร่งปฏิกิริยาช่วยเพื่อให้กลายเป็นผลิตภัณฑ์สารประกอบ oxygenate (B) แต่ทั้งนี้เวลาที่ใช้ในการออกซิไดซ์นั้นต้องเหมาะสม คือไม่มากและไม่น้อยเกินไป (ในกรณีของ tubular reactor เวลาที่ใช้ในการออกซิไดซ์ก็คือความยาวของตัว reactor หารด้วยความเร็วที่สารตั้งต้นไหลผ่าน) ในกรณีของปฏิกิริยา thermal cracking นั้น ไฮโดรคาร์บอนโมเลกุลใหญ่ที่เป็นสารตั้งต้นจะได้รับความร้อนจนโมเลกุลแตกออกเป็นโมเลกุลที่เล็กลง ตัวอย่างของปฏิกิริยานี้ได้แก่การเปลี่ยนน้ำมันหนัก (เช่นน้ำมันเตา) ให้กลายเป็นน้ำมันเบา (เช่น เบนซินและดีเซล) และการผลิตโอเลฟินส์ (เช่นเอทิลีนและโพรพิลีน)
 

ในกรณีที่เวลาที่ใช้ในการทำปฏิกิริยานั้นสั้นเกินไป สารตั้งต้น (A) ก็จะทำปฏิกิริยาไปได้ไม่มาก อาจต้องมีการติดตั้งกระบวนการนำกลับ (recycle) เพื่อนำสารตั้งต้นที่เหลือนั้นมาใช้ใหม่ แต่ถ้าใช้เวลาในการทำปฏิกิริยานานเกินไป ผลิตภัณฑ์หลักที่ต้องการ (B) จะมีการสลายตัวต่อไปเป็นผลิตภัณฑ์ที่ไม่ต้องการ (C) มากเกินไป ทำให้เกิดการสูญเสีย โดยในกรณีของปฏิกิริยา partial oxidation สาร C ก็คือ CO₂ ส่วนปฏิกิริยา thermal cracking นั้น ในกรณีของการผลิตน้ำมันเบาที่ต้องการใช้เป็นเชื้อเพลิงเหลว สาร C ก็จะเป็นพวกโมเลกุลที่เป็นแก๊ส (C₁ - C₅) และถ้าเป็นกระบวนการผลิตโอเลฟินส์ สาร C ก็จะเป็นพวก อะเซทิลีน (acetylene C₂H₂) และมีเทน (methane CH₄) เป็นต้น
 

ในกรณีของปฏิกิริยาเหล่านี้ ณ อุณหภูมิหนึ่ง ค่าคงที่ของการเปลี่ยนจาก A เป็น B (ค่า k₁) จะมีค่าสูงกว่าค่าคงที่ของการเปลี่ยนจาก B เป็น C (ค่า k₂) ดังนั้นคำถามที่มักเกิดขึ้นกับปฏิกิริยาเช่นนี้คือควรต้องใช้เวลาในการทำปฏิกิริยานานเท่าใด จึงจะได้ B มากที่สุด..."

"... ค่าคงที่อัตราการเกิดปฏิกิริยาหรือค่า k นั้นเพิ่มขึ้นตามอุณหภูมิในรูปของฟังก์ชัน exponential เมื่ออุณหภูมิการทำปฏิกิริยาเพิ่มสูงขึ้น ค่า k₁ และ k₂ ก็จะเพิ่มขึ้นตามไปด้วย การเปลี่ยนแปลงเหล่านี้ส่งผลต่อเวลาที่จะทำให้ได้ค่า B มากที่สุด ตัวอย่างเช่นในกรณีของ tubular fixed-bed catalytic reactor เมื่อใช้งานไปเรื่อย ๆ ความว่องไวในการทำปฏิกิริยาของตัวเร่งปฏิกิริยาจะลดต่ำลง ทำให้ค่า conversion ลดต่ำลง เพื่อที่จะรักษาค่า conversion ให้คงเดิม ก็อาจต้องการทำการ 
 

(ก) ลดอัตราการไหลของสารตั้งต้นให้ต่ำลง เพื่อให้มีเวลาการทำปฏิกิริยานานขึ้น และ/หรือ

(ข) เพิ่มอุณหภูมิการทำปฏิกิริยา เพื่อให้ปฏิกิริยาเกิดเร็วขึ้น 
 

ส่วนวิธีการไหนจะเหมาะสมกว่ากันนั้น คงต้องพิจารณาเป็นรายปฏิกิริยาไป ..."

ท้ายสุดก็ต้องขอต้อนรับสมาชิกใหม่ทั้ง ๓ คนของกลุ่ม ที่เปิดเทอมไปเมื่อวาน โดย Memoir ฉบับนี้จะเป็นฉบับแรกที่จัดส่งให้ทางอีเมล์ ที่จะจัดส่งให้เรื่อย ๆ จนกว่าจะถึงวันรับพระราชทานปริญญาบัตร

ดาวน์โหลดไฟล์ pdf ฉบับเต็ม กดที่ลิงค์นี้

 

รู้ทันนักวิจัย (๘) ลดความถูกต้องของการแก้สมการ เพื่อให้ผลการคำนวณตรงกับข้อมูลที่มี MO Memoir : Friday 17 November 256

"ทำไมถึงเลือกใช้วิธี Crank-Nicholson" 
  

เพราะคำถามนี้ของผม ทำให้ได้เห็นอะไรที่ไม่ชอบมาพากลในงานวิจัยทางด้าน simulation ของเขา

สำหรับผู้ที่ใช้โปรแกรมสำเร็จรูปที่ใช้ระเบียบวิธีการคำนวณเชิงตัวเลขในการแก้ปัญหาระบบสมการอนุพันธ์สามัญ ปัญหาเงื่อนไขค่าขอบเขต (Ordinary Differential Equation - Initial Value Problem หรือที่ย่อว่า ODE-IVP) เทคนิคหลักที่ใช้กันมากที่สุดเห็นจะได้แก่เทคนิคที่มีพื้นฐานมาจาก 4th order Runge-Kutta ด้วยเหตุผลที่ว่าวิธีนี้สามารถให้คำตอบที่มีความถูกต้องสูงโดยไม่จำเป็นต้องใช้ step size ที่แคบมากดังเช่นระเบียบวิธีอื่น และด้วยการที่มันเป็นวิธีการในตระกูล explicit method ทำให้การแก้สมการทำได้ง่าย (แม้ว่าจะเป็นสมการไม่เชิงเส้นก็ตาม) และเทคนิคนี้ก็สามารถแก้ปัญหาส่วนใหญ่ได้ดี
 

แต่ในกรณีที่โจทย์ที่ทำการแก้นั้นมีปัญหาเรื่องเสถียรภาพของการคำนวณ (ค่อนข้างจะไวต่อการสะสมค่าความคลาดเคลื่อน (หรือ error) ที่เกิดจากการคำนวณในแต่ละ step) การหันไปใช้วิธีการในกลุ่ม multi step หรือในตระกูล semi-implicit หรือ implicit method จะให้การควบคุมการสะสม error ที่เกิดขึ้นจากการคำนวณในแต่ละ step ที่ดีกว่า 
  

เวลาที่ผมสอบวิทยานิพนธ์งานด้าน simulation นั้น ผมจะถามผู้ทำวิจัยเสมอว่าจะเอาผลที่คำนวณได้นั้นไปทำอะไร ถ้าหากต้องการเอาไปใช้ในการออกแบบหรือเปรียบเทียบกระบวนการ ผมจะให้น้ำหนักไปที่ความถูกต้องของแบบจำลองและเทคนิคที่ใช้ในการแก้ปัญหาเป็นหลัก เรื่องเวลาที่ต้องใช้ในการคำนวณเป็นเรื่องรองลงมา (กล่าวคือแม้ว่าจะต้องใช้ step size ที่แคบ ทำให้เสียเวลาในการคำนวณมาก แต่เพื่อให้ได้คำตอบที่ถูกต้องของระบบสมการที่ตั้งขึ้น ก็เป็นสิ่งที่จำเป็นต้องทำ) แต่ถ้าจะนำไปใช้ในการควบคุมกระบวนการที่เกิดขึ้นตามเวลาจริง ผมจะให้น้ำหนักไปที่เวลาที่ต้องใช้ในการคำนวณเป็นหลัก เพราะการที่รู้ว่าจะเกิดอะไรอย่างถูกต้องแต่เมื่อเหตุการณ์จริงนั้นผ่านไปแล้ว มันไม่สามารถใช้ประโยชน์อะไรได้ การที่รู้ว่ามันจะเกิดอะไร การเปลี่ยนแปลงมีขนาดประมาณเท่าใด ก่อนที่ปรากฏการณ์นั้นจะเกิดขึ้นจริง โดยยังมีเวลาเหลือในตัดสินใจว่าจะทำอะไรเพื่อรองรับการเปลี่ยนแปลงที่จะเกิดขึ้น แม้ว่าขนาดการเปลี่ยนแปลงที่ได้จากการทำนายนั้นมีความคลาดเคลื่อนอยู่บ้างปริมาณ ก็ถือว่าเป็นเรื่องที่ยอมรับได้
 

สิ่งที่พบในการสอนสัมมนานิสิตปริญญาเอกวันนั้นคือ ดูเหมือนว่าถ้าทำการหาคำตอบจนค่าที่ได้นั้นเป็นค่าที่ถูกต้องของระบบสมการคณิตศาสตร์ที่เขาตั้งขึ้นมาเพื่อใช้อธิบายปรากฏการณ์ของกระบวนการ คำตอบที่ได้จะ "ไม่ตรง" กับข้อมูลจริงที่มีอยู่ ซึ่งแสดงให้เห็นว่าตัวระบบสมการของแบบจำลอง หรือพามิเตอร์ที่ใช้ในแบบจำลองนั้น มีความไม่ถูกต้องอยู่ ซึ่งก็ควรจะต้องไปปรับแก้ที่ตัวสมการที่สร้างขึ้น หรือไม่ก็พารามิเตอร์ที่ใช้ ซึ่งจะทำให้ไม่เพียงแต่เป็นการพิสูจน์ว่าแบบจำลองที่สร้างขึ้นและพารามิเตอร์ที่ใช้นั้นสอดรับกับปรากฏการณ์จริง แต่ยังให้ความเชื่อมั่นในการนำเอาแบบจำลองและพารามิเตอร์เหล่านั้น ไปใช้ทำนายว่าจะเกิดอะไรขึ้นบ้างเมื่อระบบได้รับการรบกวน (หรือมีการเปลี่ยนแปลง input)
 

แต่เขากลับไปใช้วิธีไปลด "ความถูกต้อง" ของคำตอบที่ได้จากการแก้ปัญหาระบบสมการ เพื่อให้ค่าที่คำนวณได้นั้น (ซึ่งประกอบด้วย คำตอบที่ถูกต้องของสมการคณิตศาตร์ที่ใช้สร้างแบบจำลอง บวกกับความคลาดเคลื่อนจากการคำนวณ) ใกล้เคียงกับข้อมูลที่มีอยู่ แล้วก็รีบอ้างว่าแบบจำลองที่สร้างขึ้นและพารามิเตอร์ที่นำมาใช้นั้น สามารถใช้แทนปรากฏการณ์จริงได้ (ด้วยการเทียบกับข้อมูลที่มีอยู่) และสามารถใช้ทำนายการเปลี่ยนแปลงของกระบวนการได้ ซึ่งเป็นสิ่งที่ไม่ถูกต้อง

รูปที่ ๑ คำตอบของสมการ dc/dt = -0.25c คือเส้นทึบสีน้ำเงิน ส่วนคำตอบที่ถูกต้องของสมการ dc/dt = -0.2c คือเส้นประสีม่วงเส้นบนสุด แต่ถ้าทำการแก้หาคำตอบของสมการ dc/dt = -0.2c ด้วยระเบียบวิธี Crank-Nicholsonและใช้ค่า Δt ต่าง ๆ กันจะพบว่าเมื่อใช้ Δt = 7 จะได้ค่าออกมาดูใกล้เคียงกับคำตอบของสมการ dc/dt = -0.25c แต่นี่ไม่ใช่การกระทำที่ถูก เพราะถ้าลดค่า Δt ลงไปเรื่อย ๆ จนคำตอบที่ได้ลู่เข้าหาคำตอบของสมการที่นำมาสร้างแบบจำลอง (คือสมการ dc/dt = -0.2c) จะพบว่าแท้จริงแบบจำลองที่นำมาใช้นั้นมีความคลาดเคลื่อนสูงอยู่ ในที่นี้วาดกราฟผลการคำนวณบนสเกล linear-log เพื่อให้เห็นภาพความแตกต่างในช่วงความเข้มข้นต่ำได้ชัดเจน

เพื่อให้เห็นภาพจะขอยกตัวอย่างโดยสมมุติว่าเรากำลังศึกษาอัตราการเกิดปฏิกิริยาของสารตั้งต้นตัวหนึ่ง ที่ค่าอัตราการเกิดปฏิกิริยาที่แท้จริงเป็นไปตามสมการ dc/dt = -0.25c (เมื่อ c คือความเข้มข้น และ t คือเวลา) ซึ่งให้ค่าความเข้มข้นของสาร ณ เวลาใด ๆ เป็นไปตามเส้นทึบสีน้ำเงินในรูปที่ ๑ แต่เรากลับไปคิดว่าอัตราการเกิดปฏิกิริยานั้นเป็นไปตามสมการ dc/dt = -0.2c (คือค่า rate constant ที่ใช้ในแบบจำลองนั้นมีค่าเพียงแค่ 80% ของค่าแท้จริง) จากนั้นก็ทำการแก้สมการ dc/dt = -0.2c ด้วยระเบียบวิธี Crank-Nicholson เพื่อหาค่า c ที่เวลาต่าง ๆ กัน ซึ่งจะได้ว่า

c(t+Δt) = c(t).(1 - 0.2.Δt/2)/(1 + 0.2.Δt/2)

ซึ่งจะพบว่าถ้าลดค่า Δt ให้ลดต่ำลง ค่าที่คำนวณได้จากระเบียบวิธี Crank-Nichloson จะลู่เข้าหาคำตอบที่ถูกต้องของสมการ dc/dt = -0.2c (คือเส้นสีม่วงในรูปที่ ๑) ซึ่งเป็นการแสดงว่าแบบจำลองที่ตั้งขึ้นนั้นมีความไม่ถูกต้องอยู่ เพราะคำตอบที่ถูกต้องของสมการที่ใช้ในการสร้างแบบจำลองนั้นให้ผลที่แตกต่างไปจากค่าที่เป็นจริง
 

แต่สิ่งที่นิสิตผู้นั้น (นิสิตปริญญาเอกปี ๔) ทำก็คือเขาไปลดค่าระดับความถูกต้องของคำตอบที่ต้องการในตัวโปรแกรมให้ลดต่ำลง (ซึ่งมันส่งผลต่อค่า step size ที่ใช้ในการคำนวณ ทำให้สามารถใช้ step size ที่กว้างขึ้น) โดยให้เหตุผลว่าเพื่อให้ผลการคำนวณที่ได้นั้นมันใกล้เคียงกับข้อมูลจริง และช่วยลดเวลาในการคำนวณ (ผลจากการที่ใช้ step size ที่กว้างขึ้น) ซึ่งการกระทำดังกล่าวเป็นการกระทำที่ไม่ถูกต้อง

และนี่ก็ไม่ใช่ครั้งแรกที่พบกับการกระทำแบบนี้

ใครตามที่คอยฟังแต่ผลและข้อสรุป โดยไม่สนใจว่าผลและข้อสรุปนั้นได้มาด้วยวิธีการอย่างไร ก็จะโดนผู้ทำวิจัยหลอก (รับประทาน) อยู่เรื่อยไป

กรุงเทพมหานครตอน ๕ โมงเย็นของวันวาน ถ่ายจากชั้น ๕ อาคารจอดรถ มองไปทางด้านทิศตะวันตกเฉียงใต้

การคำนวณเชิงตัวเลข (๒) การแก้สมการอนุพันธ์ด้วยฟังก์ชันพหุนาม MO Memoir : Monday 21 June 2553

จาก Memoir ฉบับที่แล้ว (ปีที่ ๒ ฉบับที่ ๑๗๔ เรื่อง การคำนวณเชิงตัวเลข (๑) การแก้สมการอนุพันธ์ด้วยฟังก์ชันพหุนาม) ที่ผมกล่าวไว้ว่า

ตรงนี้ขอขยายความตรงข้อความที่เน้นไว้คือ "บริเวณที่คำตอบมีการเปลี่ยนแปลงมาก" เพราะพออ่านแล้วรู้สึกว่าจะใช้คำที่มีความหมายกำกวมไปหน่อย

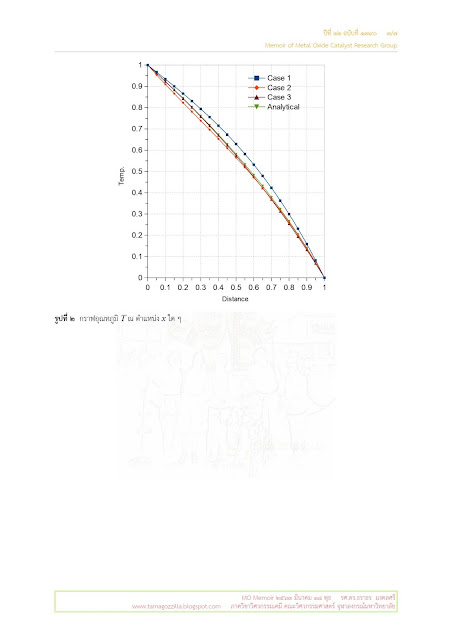
อันที่จริงแล้วควรจะกล่าวว่าเป็น "บริเวณที่เส้นกราฟของคำตอบมีการเปลี่ยนแปลงทิศทาง" หรือ "มีการเปลี่ยนความชันอย่างรวดเร็ว" อาจจะให้ความหมายที่ดีกว่า เพราะถ้าใช้คำว่า "บริเวณที่คำตอบมีการเปลี่ยนมาก" อาจทำให้เข้าใจผิดได้ว่าเป็นบริเวณที่กราฟมีความชันมาก ดังนั้นเพื่อให้เห็นภาพจึงจะขอให้พิจารณารูปที่ 1 ข้างล่าง

จากรูปที่ 1 เส้นกราฟสีเขียวจะมีตำแหน่งที่กราฟมีการเปลี่ยนทิศทางอย่างรวดเร็วอยู่บริเวณทางด้านซ้าย ส่วนเส้นกราฟสีแดงมีการเปลี่ยนทิศทางอย่างรวดเร็วอยู่บริเวณทางด้านขวา แม้ว่าทางด้านขวาของลูกศรสีน้ำเงินจะมีค่าฟังก์ชันที่เปลี่ยนแปลงมาก แต่การเปลี่ยนแปลงดังกล่าวค่อนข้างราบเรียบ (กราฟไม่ได้มีการบิดตัวมาก) ดังนั้นเพื่อให้คำตอบนั้นออกมาดีที่จุด การเลือกตำแหน่งจุด x เพื่อใช้คำนวณค่า a₂ จึงควรอยู่ที่บริเวณที่ระบุไว้ด้วยลูกศรสีน้ำเงิน ซึ่งเป็นบริเวณที่กราฟมีการเปลี่ยนแปลงทิศทางอย่างรวดเร็ว

ฟังดูมันเหมือนง่าย แต่ในความเป็นจริงนั้นมันมีปัญหาตรงที่เป็นเรื่องปรกติที่ "เรามักไม่ทราบว่ากราฟของคำตอบนั้นมันมีหน้าตาเป็นอย่างไร" ทำให้เราไม่สามารถกำหนดจุด x ที่เหมาะสมที่ควรใช้เพื่อคำนวณค่า a₂ ได้

เรื่องหน้าตาของคำตอบนี้ขอพักเอาไว้ก่อน ตอนนี้ขอย้อนกลับไปยังตัวอย่างเดิมใน Memoir ฉบับที่แล้ว (ปีที่ ๒ ฉบับที่ ๑๗๔) โดยจะทดลองดูว่าถ้าเราเปลี่ยนจุดx ที่ใช้คำนวณค่า a₂ (โดยใช้สมการที่ (11)) จาก 0.5 ไปเป็น 0.3 และ 0.7 ผลการคำนวณจะออกมาอย่างไร

กระบวนการคำนวณหาค่า a₁ และ a₂ และตรวจสอบว่าค่าใดเป็นค่าที่ถูกต้องนั้นกระทำตามวิธีที่กล่าวไว้ในบันทึกฉบับที่แล้วทุกประการ เว้นแต่เปลี่ยนค่า x เป็น 0.3 หรือ 0.7 เท่านั้นเอง ผลการคำนวณที่ได้มานั้นแสดงไว้ในตารางและรูปข้างล่าง และยังได้ทำการเปรียบเทียบ อุณหภูมิ ฟลักซ์ความร้อน และส่วนตกค้าง เมื่อเลือกจุด x ที่ใช้คำนวณค่า a₂ เป็น 0.3 0.5 และ 0.7 ไว้ในรูปที่ 4-6 ด้วย

แม้ว่าผลที่แสดงในรูปที่ 4 จะทำให้รู้สึกว่าไม่ว่าจะเลือกจุด x เป็น 0.3 0.5 หรือ 0.7 ก็ไม่ได้ทำให้ค่าอุณหภูมิที่คำนวณได้แตกต่างกันมากนั้น แต่ถ้าพิจารณาฟลักซ์ความร้อน (รูปที่ 5) หรือส่วนตกค้าง (รูปที่ 6) จะพบว่าให้ผลที่แตกต่างกันค่อนข้างมาก (ตรงนี้ขอหมายเหตุไว้นิดนึงว่า เนื่องจากเป็นการถ่ายเทความร้อนในภาวะคงตัวจากทางผนังด้านซ้าย (x = 0) ไปทางผนังด้านขวา (x = 1) ดังนั้นค่าฟลักซ์ความร้อนที่ตำแหน่ง x ใด ๆ จึงควรเท่ากันหมด กล่าวอีกนัยหนึ่งคือความร้อนที่ไหลเข้ามาจะเท่ากับความร้อนที่ไหลออกไปโดยไม่มีการสะสม)

การทำให้ส่วนตกค้างลดลงนั้นทำได้โดยการใช้ฟังก์ชันพหุนามที่มีอันดับสูงขึ้น (เช่นใช้สมการกำลัง 3 หรือกำลัง 4) ซึ่งจะทำให้เราได้ตำแหน่งที่มีค่าส่วนตกค้างเป็นศูนย์มากขึ้น หรือโดยการแบ่งช่วงการคำนวณออกเป็นช่วงย่อย ๆ ที่แคบลง เช่นแบ่งออกเป็นช่วง [0.0,0.5] และ [0.5,1.0] โดยมีสมการหนึ่งสำหรับใช้ในช่วง [0.0,0.5] และอีกสมการหนึ่งใช้ในช่วง [0.5,1.0] และใช้เงื่อนไขบังคับให้ค่าของฟังก์ชัน (และอาจรวมถึงอนุพันธ์อันดับ 1 ด้วย) ที่ตำแหน่ง x = 0.5 ของช่วง [0.0,0.5] ต่อเนื่องกับค่าของฟังก์ชันที่ตำแหน่ง x = 0.5 ของช่วง [0.5,1.0] ซึ่งตรงจุดนี้ขอพักเอาไว้ก่อนและจะแสดงให้เห็นในตอนต่อไป

การคำนวณเชิงตัวเลข (๑) การแก้สมการอนุพันธ์ด้วยฟังก์ชันพหุนาม MO Memoir : Sunday 20 June 2553

เมื่อพฤหัสที่แล้วได้พบกับนักศึกษาปริญญาเอกจากสถาบันแห่งหนึ่ง ซึ่งบังเอิญผมได้รับเชิญไปเป็นอาจารย์ที่ปรึกษาร่วมของเขา งานที่เขาทำนั้นมันคล้ายกับงานวิทยานิพนธ์ที่ผมทำตอนเรียนปริญญาโทและปริญญาเอก คือเป็นการสร้างแบบจำลองทางคณิตศาสตร์ของเครื่องปฏิกรณ์ชนิดเบดนิ่ง (fixed-bed reactor) ซึ่งตอนนั้นผมใช้วิธี orthogonal collocation ร่วมกับ finite element ในการแก้ปัญหาระบบสมการอนุพันธ์ย่อย

สมัยนั้นเวลาทำ simulation แต่ละครั้งก็ต้องเขียนโปรแกรมภาษา FORTRAN กันเอง ต้องแปลงสมการอนุพันธ์ให้อยู่ในรูประบบสมการพีชคณิตที่เหมาะสมเสียก่อน จากนั้นจึงค่อยแก้ปัญหาระบบสมการพีชคณิต ยังดีที่ตอนนั้นยังพอมี NAG Library ซึ่งเป็นซอร์ฟแวร์รวบรวม code ต่าง ๆ สำหรับแก้ปัญหาระบบสมการพีชคณิต ก็เลยไม่ต้องเขียนโปรแกรมส่วนดังกล่าว แต่ก็ต้องรู้ว่า code ตัวไหนเหมาะกับระบบสมการรูปแบบอย่างไรจะได้เลือกใช้ให้ถูก แต่ถึงกระนั้นตัวโปรแกรมก็ยาวร่วม 1000 บรรทัด

ตอนนั้นการทำ dynamic simulation พึ่งอยู่ในช่วงเริ่มต้นการพัฒนา โปรแกรมจำลองกระบวนการทางวิศวกรรมเคมีที่ขายกันอยู่ในขณะนั้นทำได้เพียงแค่ที่ภาวะคงตัว ทั้งนี้เป็นเพราะข้อจำกัดทางด้านคอมพิวเตอร์โดยเฉพาะในเรื่องของหน่วยความจำ ผมเองต้องเขียนโปรแกรมเพื่อทำ dynamic simulation เลยต้องเรียนรู้เทคนิคการแก้ปัญหาที่จะทำให้แก้ปัญหาได้รวดเร็วและใช้หน่วยความจำให้น้อยที่สุด ซึ่งวิธีที่เลือกใช้ตอนนั้นก็คือ orthogonal collocation ร่วมกับ finite element นั่นเอง

เรื่องที่นักศึกษาผู้นั้นมาปรึกษาผมคือต้องการทำความเข้าใจในเรื่องดังกล่าว (การใช้วิธี orthogonal collocation ร่วมกับ finite element ในการแก้ปัญหาระบบสมการอนุพันธ์ย่อย) แต่ปัญหาก็คือดูเหมือนว่าตำราทางด้านนี้ที่เกี่ยวข้องกับทางวิศวกรรมเคมีแทบไม่มีเลย (แม้แต่ตำราภาษาอังกฤษ) และจากประสบการณ์ของผมเองก็พบว่าตำราดังกล่าวเท่าที่มีอยู่นั้น ถ้าผู้อ่านเองไม่มีพื้นฐานทางด้านการคำนวณเชิงตัวเลขมาก่อน ก็จะอ่านเข้าใจยากหรือไม่เข้าใจเลย (ตอนที่ผมไปเรียนนั้นต้องค่อย ๆ แกะสมการทีละบรรทัดกว่าจะเข้าใจ เพราะคนเขียนเองถือว่าคนที่มาอ่านนั้นควรต้องมีความรู้พื้นฐานทางด้านการคำนวณเชิงตัวเลขอยู่ในระดับหนึ่งแล้ว) และบังเอิญตอนที่เขาจบปริญญาตรีมานั้น สถาบันที่เขาจบมาก็ไม่ได้สอนเรื่องนี้ด้วย (เขาบอกผมอย่างนั้น) ก่อนหน้านี้ผมก็เลยแนะนำเอกสารให้ไปอ่านเพื่อช่วยปูพื้นเรื่องการคำนวณเชิงตัวเลขในการแก้ปัญหาระบบสมการพีชคณิตและสมการอนุพันธ์ (ตอนนี้ก็ไม่รู้เหมือนกันว่าเขาอ่านไปถึงไหนแล้ว) มาถึงวันนั้นผมก็เลยช่วยปูพื้นให้ก่อนเบื้องต้นว่าแนวความคิดของวิธีการดังกล่าวมันมาอย่างไร

มาถึงตรงนี้สมาชิกของกลุ่มคงจะสงสัยว่าทำไมผมถึงไปยุ่งเรื่องนั้นได้ ผมไม่ได้ทำงานเกี่ยวกับเคมีวิเคราะห์หรือตัวเร่งปฏิกิริยาหรือ อันที่จริงผมก็เคยบอกไปแล้วว่าตอนเรียนโทนั้น วิทยานิพนธ์ของผมเป็นงานสร้างแบบจำลองทางคณิตศาสตร์ และตอนเรียนเอกนั้นงานวิทยานิพนธ์ก็เป็นการสร้างแบบจำลองทางคณิตศาสตร์ร่วมกับการทดลองกับ pilot plant (รูปที่อยู่ในหน้า blog นั่นแหละ)

เรื่องนี้ค่อนข้างจะยาว แต่จะพยายามเขียนเป็นตอนสั้น ๆ ซึ่งไม่รู้ว่ากี่ตอนจะจบ คาดว่าพอเขียนครบหมดก็น่าจะพิมพ์เป็นตำราขายได้ (หวังว่าคงได้ขายก่อนเกษียณอายุ) และเรื่องที่เขียนนั้นก็อาจจะไม่ต่อเนื่องเป็นลำดับ ขึ้นอยู่กับคำถามที่มีการถามเข้ามาและอารมณ์ของผู้เขียน

เรื่องแรกที่จะเขียนคือการใช้ฟังก์ชันพหุนาม (polynomial) ในการแก้ปัญหาสมการอนุพันธ์ ซึ่งจะว่าไปแล้วก็เกี่ยวข้องกับการแก้สมการโดยใช้อนุกรมอนันต์ต่าง ๆ ที่สมาชิกหลายคนต้องเรียนในวิชา Adv Math ในภาคการศึกษานี้ด้วย

สมมุติว่าเรามีการนำความร้อนจากผนังด้านหนึ่ง (x =0) ไปยังผนังอีกด้านหนึ่ง (x = 1) ที่ภาวะคงตัว สมการการนำความร้อนผ่านผนังดังกล่าวมีรูปแบบดังนี้

เนื่องจากเราไม่ทราบว่าคำตอบจะพฤติกรรมเช่นใด แต่จากเงื่อนไขค่าขอบเขตทำให้ทราบว่าอุณหภูมิทางด้านซ้าย (x = 0) นั้นสูงกว่าทางด้านขวา (x = 1) ดังนั้นค่าอุณหภูมิที่ตำแหน่ง x ใด ๆ ที่อยู่ระหว่าง 0 ถึง 1 จึงควรมีลักษณะลดลงจากซ้ายไปขวา แต่จะลดลงเป็นเส้นตรงหรือเส้นโค้งอย่างไรก็ไม่รู้ ในขั้นแรกจึงอาจเริ่มเดาโดยสมมุติให้สมการความสัมพันธ์ระหว่างอุณหภูมิ T กับตำแหน่ง x ใด ๆ เป็นไปตามฟังก์ชันพนุนามกำลัง 2 ดังนี้

T = a₀ + a₁x + a₂x² สมการ (3)

โดยที่ a₀ a₁ และ a₂ คือค่าสัมประสิทธิ์

เพื่อให้สมการที่ (3) นั้นสอดรับกับเงื่อนไขค่าขอบเขต เราจึงนำเงื่อนไขค่าขอบเขตมาแทนลงในสมการที่ (3) จากเงื่อนไขที่ว่า ณ ตำแหน่ง x = 0 ค่า T = 1 เมื่อแทนลงไปในสมการที่ (3) จะได้

a₀ = 1 สมการ (4)

และที่ตำแหน่ง x = 1 ค่า T = 0 เมื่อแทนลงไปในสมการที่ (3) จะได้

0 = 1 + a₁ + a₂

หรือ a₁ = -(1 + a₂) สมการ (5)

แทนค่าสมการที่ (4) และ (5) ลงไปใน (3) จะได้

T = 1 - (1 + a₂)x + a₂x² สมการ (6)

ซึ่งเมื่อจัดรูปแบบใหม่จะได้

T = (1 - x) + (x² - x)a₂ สมการ (7)

โดยการหาอนุพันธ์สมการที่ (6) จะได้

แทนค่าจากสมการที่ (7) (9) และ (10) ลงไปในสมการที่ (2) จะได้

[1 + (1 - x) + (x² - x)a₂](2a₂ ) + [-1 + (2 x -1)a₂]² = 0 สมการ (11)

ในขณะนี้เราติดค่าสัมประสิทธิ์ที่ไม่รู้ค่าอยู่เพียงตัวเดียวคือ a₂ ซึ่งการหาค่า a₂ ทำได้โดยการเลือกตำแหน่งค่า x มาค่าหนึ่ง (การเลือกตำแหน่งนี้ค่อนข้างเป็นอิสระหรือาจกล่าวได้ว่าเลือกตามใจชอบก็ได้ แต่โดยหลักก็คือควรเลือกให้อยู่ในบริเวณที่คำตอบมีการเปลี่ยนแปลงมาก ส่วนการเลือกตำแหน่งจะส่งผลอย่างไรต่อคำตอบนั้นคอยติดตามชมในตอนต่อไป) แล้วนำค่า x ที่เลือกมานั้นแทนลงไปในสมการที่ (11) ก็จะคำนวณหาค่าสัมประสิทธิ์ a₂ ได้

ในครั้งแรกนี้จะลองเลือกที่ตำแหน่ง x = 0.5 ซึ่งเมื่อแทนค่าลงไปในสมการที่ (11) และจัดรูปแบบใหม่จะได้

-0.5 a₂² + 3a₂ + 1 = 0 สมการ (12)

โดยการแก้สมการที่ (12) และนำค่า a₂ ที่ได้ไปคำนวณหาค่า a₁ จากสมการที่ (5) จะได้

a₁ = -0.683375 และ a₂ = -0.316625

หรือ a₁ = -7.316625 และ a₂ = 6.316625

ซึ่งจะทำให้เรามีคำตอบที่เป็นไปได้สองคำตอบคือ

T = 1 - 0.683375x - 0.316625x² สมการ (13)

หรือ T = 1 - 7.316625 x - 6.316625x² สมการ (14)

ที่นี้เราจะรู้ได้อย่างไรว่าสมการไหนเป็นสมการที่ถูกต้อง เราทำได้โดยคำนวณหาค่าฟลักซ์ความร้อน (heat flux) จากสมการ

โดยการใช้สมการที่ (13) จะได้ค่า heat flux ที่ x = 0 มีค่าเป็น 1.36675 และที่ x = 1 มีค่าเป็น 1.316625 ซึ่งแสดงให้เห็นว่าความร้อนไหลไปในทิศทางเดียวกัน (เครื่องหมายของฟลักซ์ความร้อนที่ตำแหน่งทั้งสองเหมือนกัน) แต่ถ้าใช้สมการที่ (14) จะได้ค่า heat flux ที่ x = 0 มีค่าเป็น 14.663325 และที่ x = 1 มีค่าเป็น -5.316625 ซึ่งให้ทิศทางการไหลของความร้อนที่ตำแหน่ง x = 1 ผิดจากที่ควรเป็น (กล่าวคือมีเครื่องหมายตรงข้ามกับที่ตำแหน่ง x = 0) ดังนั้นจึงสรุปได้ว่าสมการที่ถูกต้องคือสมการที่ (13) ส่วนสมการที่ (14) ก็ให้โยนทิ้งไป

การทดสอบว่าสมการที่ (13) นั้นเป็นคำตอบที่แท้จริงของสมการที่ (2) หรือว่าเป็นเพียงคำตอบโดยประมาณนั้นทำได้โดยการแทนค่าสมการที่ (13) กลับเข้าไปในสมการที่ (2) ซึ่งถ้าสมการที่ (13) เป็นคำตอบที่เป็นจริงแล้ว เราจะพบว่าเมื่อแทนค่าสมการที่ (13) กลับเข้าไปในสมการที่ (2) จะต้องได้ค่าฟังก์ชันเป็น 0 ไม่ว่าที่ตำแหน่ง x ใด ๆ ถ้าหากพบว่าค่าที่ได้นั้นไม่ได้เป็น 0 ทุกตำแหน่ง x ค่านั้นจะกล่าวเป็นส่วนตกค้าง (residual) ซึ่งส่วนตกค้างนี้เป็นตัวบอกว่าการประมาณค่านั้นใกล้เคียงความจริงมากเท่าใด ยิ่งส่วนตกค้างมีค่าน้อยเท่าใดก็แสดงว่าการประมาณค่าใกล้เคียงความจริงมากเท่านั้น ค่าอุณหภูมิ (T) ฟลักซ์ความร้อน และส่วนตกค้าง ณ ตำแหน่ง x ต่าง ๆ กันได้รวบรวมเอาไว้ในตารางที่ 1 และรูปที่ 1 ข้างล่าง

จะเห็นว่าส่วนตกค้าง (residual) นั้นจะมีค่าเป็น 0 เฉพาะตรงจุดที่เราเลือกใช้ในการคำนวณกับสมการที่ (11) เท่านั้น (ในที่นี้คือตำแหน่ง x = 0.5 ) ส่วนจุดอื่นนอกเหนือจุดนี้นั้นค่าส่วนตกค้างไม่จำเป็นต้องเป็น 0 ขนาดของพื้นที่ระหว่างเส้นกราฟของส่วนตกค้าง (เส้นสีเขียว) และแกน x เป็นตัวบอกให้ทราบว่าฟังก์ชันของเรานั้นประมาณคำตอบได้ดีเพียงใด ยิ่งพื้นที่ดังกล่าวเล็กลงมาก (หรือถ้าให้ดีก็กลายเป็นศูนย์) ก็แสดงว่าสมการที่เราเลือกมานั้นสามารถประมาณคำตอบได้ดีมากขึ้น

ฉบับนี้คงพอแค่นี้ก่อน แล้วฉบับหน้าเราค่อยมาดูกันว่าถ้าเราเลือกตำแหน่ง x เป็นค่าอื่นที่ไม่ใช่ 0.5 จะส่งผลต่อคำตอบที่ได้อย่างไร

รูปผมเองสมัยเรียนปริญญาเอก ตัวเล็ก ๆ ที่อยู่ข้างหน้าคือ micro reactor ส่วนตัวใหญ่ข้างหลังคือ pilot plant

o-Xylene to phthalic anhydride pilot plant.

Department of Chemical Engineering and Chemical Technology,

Imperial College of Science, Technology, and Medicine, University of London.

South Kensington campus, London, U.K.

March 1993.